SCATMECH > Classes and Functions > Surface Scattering Models > Bobbert_Vlieger_BRDF_Model

class Bobbert_Vlieger_BRDF_Model

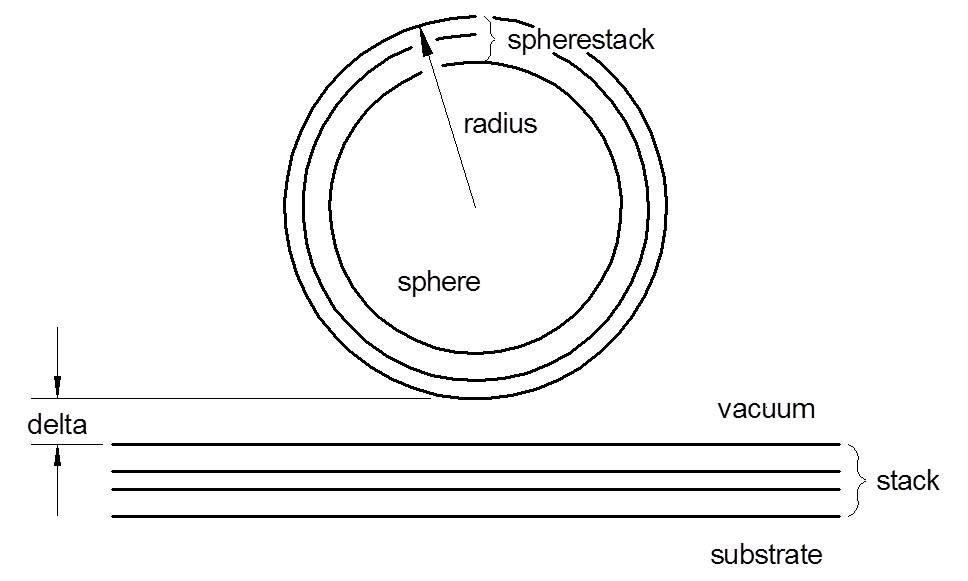
The Bobbert_Vleiger_BRDF_Model implements the theory of Bobbert and Vlieger for the scattering by a sphere on a substrate. The theory applies to a sphere of total radius radius having any number of coatings, a distance delta above a surface, which can also have any number of coatings. The sphere must lie entirely above the substrate film stack. The theory is exact, although care must be taken to choose appropriate operating parameters, and convergence should always be checked.

Parameters:

Parameter	Data Type	Description	Default
lambda	double	Wavelength of the light in vacuum [µm]. (Inherited from BRDF_Model.)	0.532
type	int	Indicates whether the light is incident from above the substrate or from within the substrate and whether the scattering is evaluated in reflection or transmission. The choices are: 0 : Light is incident from the above the substrate, and scattering is evaluated in reflection. 1 : Light is incident from the above the substrate, and scattering is evaluated in transmission. 2 : Light is incident from the within the substrate, and scattering is evaluated in reflection. 3 : Light is incident from the within the substrate, and scattering is evaluated in transmission. For 1, 2, and 3, the substrate must be non-absorbing. Bobbert_Vlieger_BRDF_Model supports all four types. (Inherited from BRDF_Model).	0
substrate	dielectric_function	The optical constants of the substrate, expressed as a complex number (n,k) or, optionally, as a function of wavelength. (Inherited from BRDF_Model.)	(4.05,0.05)
density	double	The surface number density of local scatterers [µm^-2]. (Inherited from Local_BRDF_Model.)	1
sphere	dielectric_function	The optical constants of the particle, expressed as a complex number (n,k) or, optionally, as a function of wavelength.	(1.59,0)
radius	double	The total radius of the spherical particle [µm]. This radius includes the thickness of any coatings.	0.05
spherecoat	StackModel_Ptr	Description of any stack of coatings on the particle.	No_StackModel
stack	StackModel_Ptr	Description of any stack of films deposited on the substrate.	No_StackModel
delta	double	The distance between the particle and the substrate [µm]. This value is zero when the particle is touching the substrate. It cannot be less than zero.	0
lmax	int	Maximum spherical harmonic order used in the calculation. Setting this value to 0 sends a request to use the value appropriate for the free-space particle, as suggested by Bohren and Huffman. For negative values of lmax, the lmax appropriate for the free-space particle is increased by the absolute value of lmax. For an accurate solution, convergence should be checked by varying this parameter.	0
order	int	The perturbative order for the solution. For the exact solution, the order should be set to -1. When order is set to 0, the model reproduces the Double_Interaction_BRDF_Model with a MieScatterer. When order is set to 1 or higher, matrix inversion is performed by successive approximation. This parameter is included in the model, but should normally be set to -1 for the exact solution.	-1
Norm_Inc_Approx	int	A flag indicating whether or not to use the Normal Incidence Approximation in the calculation. This approximation assumes that the reflection coefficients of the substrate are constant and given by their normal incidence values. This approximation is valid for a perfectly reflecting metallic substrate, or if the distance of the particle from the surface is large. This approximation is included for pedagogical reasons, and the flag should be set to 0 for an accurate solution. See the reference by Videen for details.	0
improve	int	The number of iterative improvement iterations. For l_max much larger than that needed for the free-space Mie scattering solution, the matrix inversion accumulates some significant errors that propagate to the final scattering solution. Setting this value to something other than 0 increases the computation time needed for each different incident angle but improves the solution stability significantly. A value of 2 or 3 has been found to be satisfactory under all tested conditions.	3

Include file:

#include "bobvlieg.h"

Source code:

bobvlieg1.cpp
bobvlieg2.cpp
bobvlieg3.cpp

Definition of public elements:

class Bobbert_Vlieger_BRDF_Model
   : public Local_BRDF_Model
{
   complex<double> Epp(double thetai,double thetas,double phis);
   complex<double> Eps(double thetai,double thetas,double phis);
   complex<double> Esp(double thetai,double thetas,double phis);
   complex<double> Ess(double thetai,double thetas,double phis);

   MuellerMatrix Specular(double theta);
};

complex<double> Epp(double thetai,double thetas,double phis)
complex<double> Eps(double thetai,double thetas,double phis)
complex<double> Esp(double thetai,double thetas,double phis)
complex<double> Ess(double thetai,double thetas,double phis)

Routines which return the elements of the Jones matrix for scattering from a sphere on a surface. These elements are the same as those calculated by jonesDSC, and these routines provide a means for obtaining each term individually.

Top of Page

MuellerMatrix Specular(double theta)

This function returns the Mueller matrix specular reflectance (for type==0 or type==2 or the regular transmittance (for type==1 or type==3) for an incident angle of theta (in radians). The result is derived from the optical theorem and is only valid when density is suffiently low that multiple scattering between spheres can be neglected.
Example:
    Bobbert_Vlieger_BRDF_Model model;
    model.set_type(0);
    MuellerMatrix R = Specular(theta);

Top of Page

For More Information

SCATMECH Technical Information and Questions
Sensor Science Division Home Page
Sensor Science Division Inquiries
Website Comments

Current SCATMECH version: 7.22 (April 2021)