steppyngstounes.pidStepper

Classes

class steppyngstounes.pidStepper.PIDStepper(start, stop, size=None, minStep=None, inclusive=False, record=False, limiting=True, proportional=0.075, integral=0.175, derivative=0.01)

Bases: Stepper

Adaptive stepper using a PID controller.

Calculates a new step as

\[\Delta_{n+1} = \left(\frac{e_{n-1}}{e_n}\right)^{k_P} \left(\frac{1}{e_n}\right)^{k_I} \left(\frac{e_{n-1}^2}{e_n e_{n-2}}\right)^{k_D} \Delta_n\]

where \(\Delta_n\) is the step size for step \(n\) and \(e_n\) is the error at step \(n\). \(k_P\) is the proportional coefficient, \(k_I\) is the integral coefficient, and \(k_D\) is the derivative coefficient.

On failure, retries with

\[\Delta_n = \mathrm{min}\left(\frac{1}{e_n}, 0.8\right) \Delta_n\]

Based on:

@article{PIDpaper,
   author =  {A. M. P. Valli and G. F. Carey and A. L. G. A. Coutinho},
   title =   {Control strategies for timestep selection in finite
              element simulation of incompressible flows and
              coupled reaction-convection-diffusion processes},
   journal = {Int. J. Numer. Meth. Fluids},
   volume =  47,
   year =    2005,
   pages =   {201-231},
   doi =     {10.1002/fld.805},
}

Note

For those familiar with PID control in other contexts, the process variable here is the normalized error, the set point is 1, and the controller output is the timestep. When the normalised error falls below 1, the controller increases the timestep. When the normalised error rises above 1, the controller decreases the timestep. You should therefore calculate your normalized error as the ratio of actual error to target error.

Parameters:

• start (float) – Beginning of range to step over.

• stop (float) – Finish of range to step over.

• size (float) – Suggested step size to try (default None).

• inclusive (bool) – Whether to include an evaluation at start (default False)

• record (bool) – Whether to keep history of steps, errors, values, etc. (default False).

• limiting (bool) – Whether to prevent error from exceeding 1 (default True).

• minStep (float) –

  Smallest step to allow (default (stop - start) * eps).

• proportional (float) – PID control \(k_P\) coefficient (default 0.075).

• integral (float) – PID control \(k_I\) coefficient (default 0.175).

• derivative (float) – PID control \(k_D\) coefficient (default 0.01).

Examples

>>> import numpy as np
>>> from steppyngstounes import PIDStepper

We’ll demonstrate using an artificial function that changes abruptly, but smoothly, with time,

\[\tanh\frac{\frac{t}{t_\mathrm{max}} - \frac{1}{2}} {2 w}\]

where \(t\) is the elapsed time, \(t_\mathrm{max}\) is total time desired, and \(w\) is a measure of the step width.

>>> totaltime = 1000.
>>> width = 0.01

The scaled “error” will be a measure of how much the solution has changed since the last step, | new - old | / errorscale).

>>> errorscale = 1e-2

Iterate over the stepper from start to stop (inclusive of calculating a value at start).

>>> old = -1.
>>> stepper = PIDStepper(start=0., stop=totaltime, inclusive=True,
...                      record=True)
>>> for step in stepper:
...     new = np.tanh((step.end / totaltime - 0.5) / (2 * width))
...
...     error = abs(new - old) / errorscale
...
...     if step.succeeded(value=new, error=error):
...         old = new

>>> s = "{} succesful steps in {} attempts"
>>> print(s.format(stepper.successes.sum(),
...                len(stepper.steps)))
283 succesful steps in 351 attempts

>>> steps = stepper.steps[stepper.successes]
>>> ix = steps.argsort()
>>> values = stepper.values[stepper.successes][ix]
>>> errors = abs(values[1:] - values[:-1]) / errorscale

Check that the post hoc error satisfies the desired tolerance.

>>> print(max(errors) < 1.)
True

(Source code)

(Source code, png, hires.png, pdf)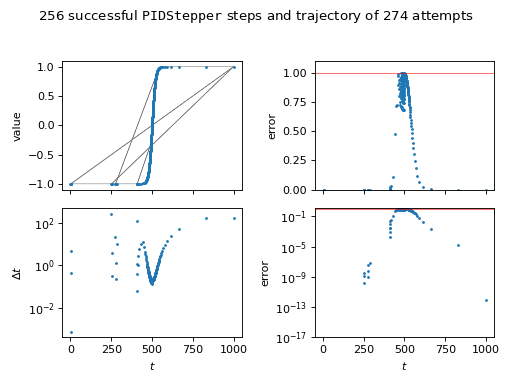

property errors

ndarray of the “error” at each step attempt.

The user-determined “error” scalar value (positive and normalized to 1) at each step attempt is passed to Stepper via succeeded().

next()

Return the next step.

Note

Legacy Python 2.7 support.

Return type:

Step

Raises:

StopIteration – If there are no further steps to take

property sizes

ndarray of the step size at each step attempt.

property steps

ndarray of values of the control variable attempted so far.

succeeded(step, value=None, error=None)

Test if step was successful.

Stores data about the last step.

Parameters:

• step (Step) – The step to test.

• value (float, optional) – User-determined scalar value that characterizes the last step. Whether this parameter is required depends on which Stepper is being used. (default None).

• error (float, optional) – User-determined error (positive and normalized to 1) from the last step. Whether this parameter is required depends on which Stepper is being used. (default None).

Returns:

Whether step was successful.

Return type:

bool

property successes

ndarray of whether the step was successful at each step attempt.

property values

ndarray of the “value” at each step attempt.

The user-determined scalar value at each step attempt is passed to Stepper via succeeded().