steppyngstounes.parsimoniousStepper

Classes

class steppyngstounes.parsimoniousStepper.ParsimoniousStepper(start, stop, N, minStep=0.0, inclusive=False, scale='dl', minsteps=4, maxinitial=11)

Bases: Stepper

Non-monotonic stepper that samples sparsely explored regions

Computes the function where the curvature is highest and where not many points have been computed.

Note

By its nature, this Stepper must record.

Parameters:

• start (float) – Beginning of range to step over.

• stop (float) – Finish of range to step over.

• N (int) – Number of points to sample.

• minStep (float) –

  Smallest step to allow (default (stop - start) * eps).

• inclusive (bool) – Whether to include an evaluation at start (default False)

• scale (str) – Parameter to indicate whether to scale by value “dy” or arc length “dl” (default “dl”).

• minsteps (int) – Minimum number of steps to take (default 4).

• maxinitial (int) – The maximum number of even steps to take before adapting (default 11).

Examples

>>> import numpy as np
>>> from steppyngstounes import ParsimoniousStepper

We’ll demonstrate using an artificial function that changes abruptly, but smoothly, with time,

\[\tanh\frac{\frac{t}{t_\mathrm{max}} - \frac{1}{2}} {2 w}\]

where \(t\) is the elapsed time, \(t_\mathrm{max}\) is total time desired, and \(w\) is a measure of the step width.

>>> totaltime = 1000.
>>> width = 0.01

The scaled “error” will be a measure of how much the solution has changed since the last step, | new - old | / errorscale).

>>> errorscale = 1e-2

Iterate over the stepper from start to stop (inclusive of calculating a value at start).

>>> stepper = ParsimoniousStepper(start=0., stop=totaltime, inclusive=True,
...                               N=50)
>>> for step in stepper:
...     new = np.tanh((step.end / totaltime - 0.5) / (2 * width))
...
...     _ = step.succeeded(value=new)

>>> s = "{} succesful steps in {} attempts"
>>> print(s.format(stepper.successes.sum(),
...                len(stepper.steps)))
50 succesful steps in 50 attempts

>>> steps = stepper.steps[stepper.successes]
>>> ix = steps.argsort()
>>> values = stepper.values[stepper.successes][ix]
>>> errors = abs(values[1:] - values[:-1]) / errorscale

As this stepper doesn’t use the error, we don’t expect the post hoc error to satisfy the tolerance.

(Source code)

(Source code, png, hires.png, pdf)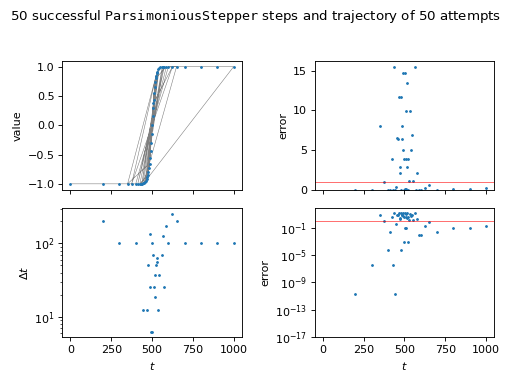

property errors

ndarray of the “error” at each step attempt.

The user-determined “error” scalar value (positive and normalized to 1) at each step attempt is passed to Stepper via succeeded().

next()

Return the next step.

Note

Legacy Python 2.7 support.

Return type:

Step

Raises:

StopIteration – If there are no further steps to take

property sizes

ndarray of the step size at each step attempt.

property steps

ndarray of values of the control variable attempted so far.

succeeded(step, value=None, error=None)

Test if step was successful.

Stores data about the last step.

Parameters:

• step (Step) – The step to test.

• value (float, optional) – User-determined scalar value that characterizes the last step. Whether this parameter is required depends on which Stepper is being used. (default None).

• error (float, optional) – User-determined error (positive and normalized to 1) from the last step. Whether this parameter is required depends on which Stepper is being used. (default None).

Returns:

Whether step was successful.

Return type:

bool

property successes

ndarray of whether the step was successful at each step attempt.

property values

ndarray of the “value” at each step attempt.

The user-determined scalar value at each step attempt is passed to Stepper via succeeded().