Basics of RME Propagation

This is a basic example demonstrating how to propagate RMEMeas objects through functions.

This example generates a hypothetical voltage and current measurement each with a Monte Carlo distribution and single linear uncertainty mechanism.

We define a propagator and a propagation function to calculate power and perform the uncertainty analysis.

Importing packages

For this example we only need RMEMeas objects and the RME propagator.

from rmellipse.uobjects import RMEMeas
from rmellipse.propagators import RMEProp

Creating a propagator

The first step is to define a propagator. This is the object that inspects functions for uncertainty objects, propagating them according to its settings.

N = 1000

myprop = RMEProp(montecarlo_sims=N, sensitivity=True)

Creating RMEMeas objects

RMEMeas objects (Rocky Mountain Ellipse Measurements) carry along with them 2 key attributes .cov and RMEMeas.mc, along attributes for propagating metadata - RMEMeas.covcats and RMEMeas.covdofs.

The`RMEMeas.cov`is an xarray.DataArray object that stores both the nominal value of the measurement, and copies of the nominal value perturbed by 1 standard deviation for each uncertainty mechanism. The perturbed copies are stored along the first dimension of the`RMEMeas.cov`attribute, which is always called ‘umech_id’. Along that dimension the first index is always labeled ‘nominal’ and holds the nominal value, the remaining indexes store the names of the linear uncertainty mechanisms. These are labelled to be unique. Importantly, if two RMEMeas objects being propagated share an uncertainty mechanism with the same umech_id (i.e. they both have a perturbed copy of the nominal with the same index label), then they are assume to be fully correlated.

The`RMEMeas.mc` attribute stores the monte-carlo data. It is also an xarray.DataArray, where the first dimension is always called umech_id, and the first index of the dimension represents the nominal value. However, the index is instead a numeric index, starting at zero and counting up. Indexes starting from 1 and up of this dimension represent samples of the probability distribution of the measurement. The RMEMeas will randomly sample from this distribution to perform the monte-carlo analysis.

In this case, we will create a voltage and current measurement, both drawing from a gaussian distribution. Because we are creating a measurement using a float, the resulting`RMEMeas.cov`attribute will be shape (2,) (index 0 for the nominal value and index 1 representing the uncertainty associated with the Gaussian we sampled from). The`RMEMeas.mc` attribute will have shape (1001,) (index 0 for the nominal and index 1-1001 representing the samples from the gaussian distribution)

use_sample_mean = False

V = RMEMeas.from_dist(
    name='voltage',
    nom=2,
    std=0.01,
    samples=N,
    dist='gaussian',
    use_sample_mean=False
)

I = RMEMeas.from_dist(
    name='current',
    nom=1.5,
    std=0.01,
    samples=N,
    dist='gaussian',
    use_sample_mean=False
)

print(V)
print('            dimensions of V.cov :', V.cov.dims, V.cov.shape)
print('             dimensions of V.mc :', V.mc.dims, V.mc.shape)
print('V linear uncertainty mechanisms :', V.umech_id)

voltage with nominal:
<xarray.DataArray ()> Size: 8B
array(2.)
            dimensions of V.cov : ('umech_id',) (2,)
             dimensions of V.mc : ('umech_id',) (1001,)
V linear uncertainty mechanisms : ['voltage_gaussian']

Propagating Through a Function

Writing a function to be propagated requires a little knowledge about how the propagator works, but in trade enables you to take advantage of vectorized operations for significantly faster computation.

First we define a function and wrap it the myprop.propagator decorator. This is equivalent to calling power = myprop.propagate(power) after defining the function power. This will tell the propagator to inspect the arguments of power when it is called and propagate any RMEMeas objects that are positional or keyword arguments.

The propagator will call the function twice. Once for the linear sensitivity analysis where it passes in the`RMEMeas.cov`attribute, and once for the monte-carlo analysis where it passes in the`RMEMeas.mc` attribute.

In the case of the sensitivity analysis, the propagator will align the linear uncertainty mechanisms of each RMEMeas object so that they can be used in math operations. In this example this means that the shape of the v and i arguments will have shape (3,) each, with the first axis aligning the uncertainty mechanisms that existed in both v and i. Uncertainty mechanisms that don’t exist in a variable are filled with a copy of the nominal in the newly aligned dimension.

For the Monte Carlo analysis, the propagator will pick random samples from the data stored in the`RMEMeas.mc` attribute. We defined 1000 montecarlo sims in our propagator so v and i will have shape (1001,) when passed through our power function ( 1000 random samples and 1 copy of the nominal value).

Note that while the propagator is design to encourage vectorization for efficiency, if that is not possible simply you can turn off vectorization with the vectorize setting. See the example on non-vectorized propagation for more details.

The propagator will name your RMEMeas object using the name of the function you used to propagate it.

@myprop.propagate
def power(v, i):
    print(v.dims, v.shape, i.shape)
    return v * i


# when we call this, note that the power function is called twice, and the shapes
# of the v and i arguments are changed from the original definitions for the
#`RMEMeas.cov`attribute, now (3,) after the uncertainty mechanisms were aligned.
p = power(V, I)

('umech_id',) (3,) (3,)
('umech_id',) (1001,) (1001,)

Evaluating Uncertainty

We can calculate the standard uncertainty of a RMEMeas object easily!

covunc, mcunc = p.stdunc(k=1)


print('sensitivity analysis uncertainty:', covunc)
print('monte-carlo uncertainty:', mcunc)

sensitivity analysis uncertainty: <xarray.DataArray ()> Size: 8B
array(0.025)
monte-carlo uncertainty: <xarray.DataArray ()> Size: 8B
array(0.02546139)

We can easily calculate the lower/upper uncertainty bounds for a given expansion factor on the uncertainty, degrees of freedom based on the linear sensitivity analysis, and confidence intervals based on the linear sensitivity analysis.

lower, upper = p.uncbounds(k=2)
dof = p.dof()
lower, upper = p.confint(0.95)

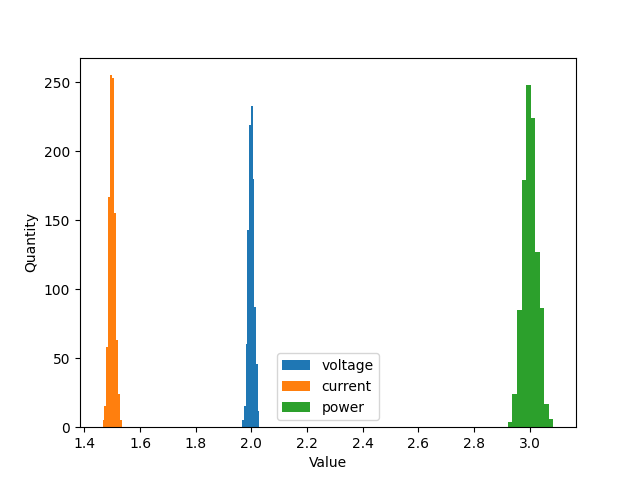
We can plot the montecarlo distributions of our results as well.

import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
ax.hist(V.mc[1:], label=V.name)
ax.hist(I.mc[1:], label=I.name)
ax.hist(p.mc[1:], label=p.name)
ax.legend(loc='best')
ax.set_xlabel('Value')
ax.set_ylabel('Quantity')

Text(38.347222222222214, 0.5, 'Quantity')