SOL Calibration

This example a performs a short, open, and load (SOL) calibration with a linear sensitivity analysis.

In this scenario, we have some raw S-parameter measurements stored in tab separated text files of our calibration standards and of our DUT - which is a load. We also have some data-defined models of our calibration standards stored in the HDF5 format. These models contain some linear uncertainty mechanisms which carry some category information describing their origin. This tutorial will walk through defining file reader functions, analysis functions, and performing the analysis with and without uncertainties.

The data for this example is stored in th ‘sol_demo_data’ folder of the source code repository hosted on github. The data set is intended to act as an example use case of the software library only.

from rmellipse.uobjects import RMEMeas
from rmellipse.propagators import RMEProp
import h5py
import numpy as np
import xarray as xr

Demo Data

The sample data are store inside the rmellipse.sol_demo submodule, and the paths to the files can be imported as well.

# text files paths as Path objects
# replace these with the correct data paths
# after downloading the sample data
short_raw_path = sample_data_dir / 'Short.s1p'
open_raw_path = sample_data_dir / 'Open.s1p'
load_raw_path = sample_data_dir / 'Load.s1p'
dut_raw_path = sample_data_dir / 'Dut.s1p'

# HDF5 file containing the standard models
defs_path = sample_data_dir/'definitions.hdf5'

Writing Functions

The first thing we need to do is write some functions. These include the text file reader and analysis functions to calculate our error box and correct our raw data.

Text File Reader

First we define a function that can read our text files into a DataArray. We assign a dimension called Frequency (GHz), where we store the frequencies corresponding to each S-parameter. We also store our data as a complex-valued array.

def from_s1p(path) -> xr.DataArray:
    arr = np.loadtxt(path, float, delimiter = '\t')
    # define a coordinate set
    coords = {
        'Frequency (GHz)': arr[:,0]
        }
    # convert to 1 port complex data
    values = arr[:,1] + 1.0j*arr[:,2]
    # create an xarray data set
    out = xr.DataArray(
        values,
        coords = coords,
        dims = ('Frequency (GHz)')
    )
    return out

Lets confirm this works by reading in our raw measurements

raw_dut = from_s1p(dut_raw_path)
raw_short = from_s1p(short_raw_path)
raw_open = from_s1p(open_raw_path)
raw_load = from_s1p(load_raw_path)

Calculating the Error Box

We want two analysis functions. The first takes in our definitions and raw measurements, and calculates the error-box terms of the 1-port calibration. Importantly, all the import objects that might be RMEMeas objects are exposed as input arguments. The ** packs any keyword arguments ino a dictionary. This function matches any inputs by matching device_names, and assuming keywords are formatted by ‘def_<device_name>’ and ‘meas_<device_name>’ only. Also, note that the function signature says that the function is expecting xr.DataArray objects. This is what will be passed in when the function is wrapped in a propagator.

def SOL_cal(**stds: xr.DataArray) -> xr.DataArray:
    # get list of standards and definitions, ordered to correspond
    defs = []
    ms = []
    for k, v in stds.items():
        if 'def' in k:
            def_key = k
            m_key = def_key.replace('def_', 'raw_')
            defs.append(stds[def_key])
            ms.append(stds[m_key])
    N = len(defs)
    frequencies = ms[-1]['Frequency (GHz)']

    # output has the same shape as the inputs except an
    # additional dimensions to hold the error terms
    output_shape = list(ms[0].shape)+[3]
    output_dims =  list(ms[0].dims) + ['errterm']
    output_coords = dict(ms[0].coords)
    output_coords.update({'errterm':['e00','e11','delta']})

    # pre allocate output xarray
    # 3 output has 3
    result = np.zeros(output_shape, complex)
    result = xr.DataArray(
        result,
        dims = output_dims,
        coords = output_coords
        )

    # pre allocated temporary arrays
    # that will be used to solve the set of equations
    mshape = list(result.shape)[:-1] + [N, 3]
    M = np.zeros(mshape, complex)

    yshape = list(result.shape)[:-1] + [N, 1]
    y = np.zeros(yshape, complex)

    # I am going to work with the underlying numpy arrays
    # here because it is convenient for linear algebra
    # for each device add a row to the regressor matrix
    for i in range(N):
        S11_meas = ms[i].values
        S11_def = defs[i].values
        M[..., i, 0] = 1
        M[..., i, 1] = S11_meas * S11_def
        M[..., i, 2] = -S11_def
        y[..., i, 0] = S11_meas

    # this transposes M along last 2 dimensions
    n_dims = len(M.shape)
    transpose_dims = np.arange(n_dims)
    transpose_dims[[n_dims - 1, n_dims - 2]] = transpose_dims[[n_dims - 2, n_dims - 1]]
    Mt = np.transpose(M, transpose_dims)

    # do least squares
    coeff = np.linalg.inv(Mt @ M) @ Mt @ y

    # reassign values to output
    result.loc[..., 'e00'] = coeff[..., 0, 0]
    result.loc[..., 'e11'] = coeff[..., 1, 0]
    result.loc[..., 'delta'] = coeff[..., 2, 0]

    return result

Lets use the function without any uncertainty propagation to verify it works. I will do this by reading in the definitions and grabbing just a view into the underlying nominal DataArray.

with h5py.File(defs_path,'r') as f:
    def_short = RMEMeas.from_h5(f['Short']).nom
    def_open = RMEMeas.from_h5(f['Open']).nom
    def_load = RMEMeas.from_h5(f['Load']).nom

flist = raw_short['Frequency (GHz)']
errbox = SOL_cal(
    def_short = def_short,
    def_open = def_open,
    def_load = def_load,
    raw_short = raw_short,
    raw_open  = raw_open,
    raw_load = raw_load
)

print(errbox)

C:\Users\dcg2\AppData\Local\Temp\1\tmps8r3znms\d7af01cdebe95d15ae90b93035c551076e223283\docs\examples\Examples\plot_e00_SOL.py:175: DeprecationWarning: from_h5() is deprecated and will be removed in 0.5.0, use rmellipse.utils.load_object instead.
  def_short = RMEMeas.from_h5(f['Short']).nom
C:\Users\dcg2\AppData\Local\Temp\1\tmps8r3znms\d7af01cdebe95d15ae90b93035c551076e223283\docs\examples\Examples\plot_e00_SOL.py:176: DeprecationWarning: from_h5() is deprecated and will be removed in 0.5.0, use rmellipse.utils.load_object instead.
  def_open = RMEMeas.from_h5(f['Open']).nom
C:\Users\dcg2\AppData\Local\Temp\1\tmps8r3znms\d7af01cdebe95d15ae90b93035c551076e223283\docs\examples\Examples\plot_e00_SOL.py:177: DeprecationWarning: from_h5() is deprecated and will be removed in 0.5.0, use rmellipse.utils.load_object instead.
  def_load = RMEMeas.from_h5(f['Load']).nom
<xarray.DataArray (Frequency (GHz): 341, errterm: 3)> Size: 16kB
array([[-0.01893933-0.03268189j, -0.05556275+0.11455476j,
         0.00717613-0.79476367j],
       [ 0.00823574-0.01836123j,  0.04484499+0.0895194j ,
        -0.71682196-0.43896957j],
       [ 0.03634635-0.02636921j,  0.06262164-0.00655716j,
        -0.69776178+0.44672811j],
       ...,
       [-0.09579545-0.01372783j, -0.09339595+0.03935082j,
         0.41148441+0.6320167j ],
       [-0.09774565+0.04137535j,  0.02886021-0.02463072j,
         0.73391962+0.00871807j],
       [-0.06464375+0.08107921j, -0.09782635-0.1258208j ,
         0.43446894-0.5824696j ]], shape=(341, 3))
Coordinates:
  * Frequency (GHz)  (Frequency (GHz)) float64 3kB 18.0 18.02 ... 26.48 26.5
  * errterm          (errterm) <U5 60B 'e00' 'e11' 'delta'

Correcting Raw Data

Finally, lets write a function that takes in our error box and corrects a raw measurement.

def SOL_correct(errorbox: xr.DataArray, device: xr.DataArray) -> xr.DataArray:
    S11 = device
    e00 = errorbox.sel(errterm="e00")
    e11 = errorbox.sel(errterm="e11")
    delta = errorbox.sel(errterm="delta")

    corrected = (-e00 + S11) / (-delta + e11 * S11)

    # return the corrected result
    r = xr.zeros_like(device)
    r.loc[...] = corrected
    return r

And lets use it to correct our raw device.

dut = SOL_correct(errbox, raw_dut)

We can plot this to check that it matches our expectations. This DUT is a load so we expect a magnitude close to 0.

import matplotlib.pyplot as plt
plt.close('all')
fig, ax = plt.subplots(2,1)
fig.suptitle('DUT Corrected Data')
ax[0].plot(dut['Frequency (GHz)'], np.abs(dut))
ax[0].set_ylabel('Linear Magnitude')

ax[1].plot(dut['Frequency (GHz)'], np.angle(dut, deg = True))
ax[1].set_xlabel('Frequency (GHz)')
ax[1].set_ylabel('Phase (deg)')

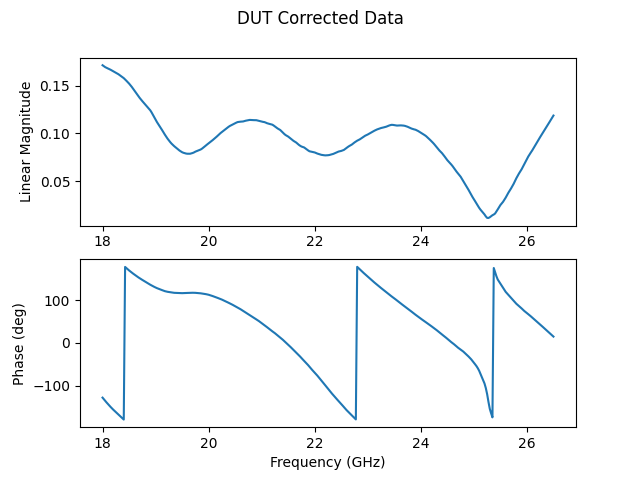
Text(26.722222222222214, 0.5, 'Phase (deg)')

Linear Uncertainty Analysis

In this step, we will add the ability to propagate uncertainties associated with the calibration standard definitions.

Import and Wrap Functions

The first step is to define a propagator and wrap our analysis functions in it. We are going to turn on the sensitivity analysis only. When we wrap our functions in the propagator, any RMEMeas objects passed through the function will be run through the linear sensitivity analysis.

from rmellipse.uobjects import RMEMeas
from rmellipse.propagators import RMEProp
import h5py
import xarray as xr
import numpy as np

myprop = RMEProp(
    sensitivity = True
    )

SOL_cal = myprop.propagate(SOL_cal)
SOL_correct = myprop.propagate(SOL_correct)

# turn xarray's into uncertainty objects with RMEMeas
raw_dut = RMEMeas.from_nom('DUT',raw_dut)
raw_short = RMEMeas.from_nom('DUT',raw_short)
raw_open = RMEMeas.from_nom('DUT',raw_open)
raw_load = RMEMeas.from_nom('DUT',raw_load)

Lets also grab our definitions with the full uncertainty information

with h5py.File(defs_path,'r') as f:
    def_short = RMEMeas.from_h5(f['Short'])
    def_open = RMEMeas.from_h5(f['Open'])
    def_load = RMEMeas.from_h5(f['Load'])

C:\Users\dcg2\AppData\Local\Temp\1\tmps8r3znms\d7af01cdebe95d15ae90b93035c551076e223283\docs\examples\Examples\plot_e00_SOL.py:269: DeprecationWarning: from_h5() is deprecated and will be removed in 0.5.0, use rmellipse.utils.load_object instead.
  def_short = RMEMeas.from_h5(f['Short'])
C:\Users\dcg2\AppData\Local\Temp\1\tmps8r3znms\d7af01cdebe95d15ae90b93035c551076e223283\docs\examples\Examples\plot_e00_SOL.py:270: DeprecationWarning: from_h5() is deprecated and will be removed in 0.5.0, use rmellipse.utils.load_object instead.
  def_open = RMEMeas.from_h5(f['Open'])
C:\Users\dcg2\AppData\Local\Temp\1\tmps8r3znms\d7af01cdebe95d15ae90b93035c551076e223283\docs\examples\Examples\plot_e00_SOL.py:271: DeprecationWarning: from_h5() is deprecated and will be removed in 0.5.0, use rmellipse.utils.load_object instead.
  def_load = RMEMeas.from_h5(f['Load'])

Propagate Functions

Now we can use our analysis functions that were wrapped in the propagator to do our analysis.

errbox = SOL_cal(
    def_short = def_short,
    def_open = def_open,
    def_load = def_load,
    raw_short = raw_short,
    raw_open  = raw_open,
    raw_load = raw_load
)

dut = SOL_correct(errbox, raw_dut)

Plot Results

Lets plot our corrected device like last time, and lets instead inspect the uncertainty measurements. We would like to look at the magnitude and phase, so lets define some functions to propagate those conversions.

Nominal Values

@myprop.propagate
def calc_mag(arr):
    out = xr.zeros_like(arr, dtype = float)
    out.values = np.abs(arr)
    return out

@myprop.propagate
def calc_phase(arr):
    out = xr.zeros_like(arr, dtype = float)
    out.values = np.angle(arr, deg = True)
    return out

mag = calc_mag(dut)
phase = calc_phase(dut)

import matplotlib.pyplot as plt
import numpy as np
k = 2
fig, ax = plt.subplots(2,1)
mag_lower = mag.uncbounds(k = k).cov
mag_upper = mag.uncbounds(k = -k).cov
phs_lower = phase.uncbounds(k = k, deg = True).cov
phs_upper = phase.uncbounds(k = -k, deg = True).cov

ax[0].fill_between(
    dut.nom['Frequency (GHz)'],
    y1 = mag_lower,
    y2 = mag_upper,
    color = 'k',
    alpha = 0.5,
    label = f'k = {k} Uncertainty'
    )

ax[1].fill_between(
    dut.nom['Frequency (GHz)'],
    y1 = phs_lower,
    y2 = phs_upper,
    alpha = 0.5,
    color = 'k',
    label = f'k = {k} Uncertainty'
    )

ax[0].plot(
    mag.nom['Frequency (GHz)'],
    mag.nom,
    label = 'nominal'
    )
ax[0].set_ylabel('Linear Magnitude')

ax[1].plot(
    phase.nom['Frequency (GHz)'],
    phase.nom,
    label = 'nominal'
    )
ax[1].set_xlabel('Frequency (GHz)')
ax[1].set_ylabel('Phase (deg)')

handles, labels = ax[0].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper center', ncols = 3)

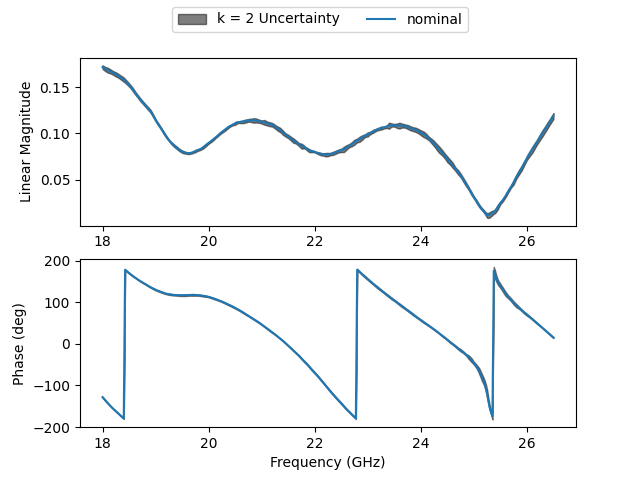
<matplotlib.legend.Legend object at 0x0000020D20B1AF90>

Uncertainties Only

Lets look at the k=2 uncertainties only. Notice how the phase uncertainty increases as the magnitude approaches zero. This is natural, as phase is not well defined if your magnitude is on the origin.

fig, ax = plt.subplots(2,1)
ax[0].plot(
    mag.nom['Frequency (GHz)'],
    mag.stdunc(k=k).cov,
    )
ax[0].set_ylabel(f'Lin Magn k={k} Uncertainty')
ax[1].plot(
    phase.nom['Frequency (GHz)'],
    phase.stdunc(k=k).cov,
    label = 'nominal'
    )
ax[1].set_xlabel('Frequency (GHz)')
ax[1].set_ylabel(f'Phase k={k} Uncertainty (deg)')

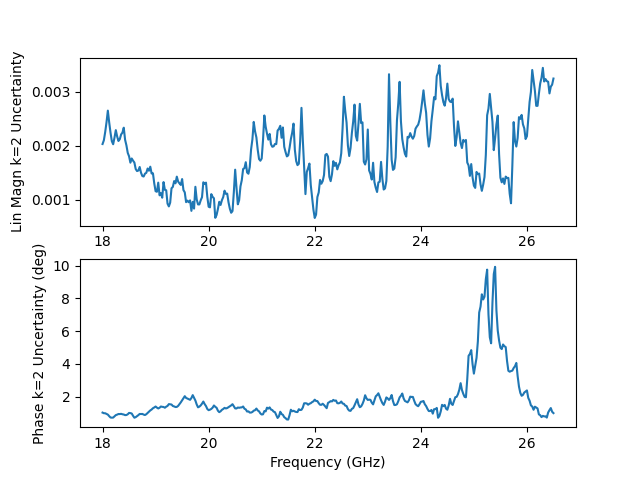
Text(47.097222222222214, 0.5, 'Phase k=2 Uncertainty (deg)')

Categorizing Uncertainties

The definitions we use have some string metadata attached to each uncertainty mechanisms. This metadata is stored in dut.covcats. Each linear uncertainty mechanism has been given an “Origin” designation we can use to group each mechanisms that belongs to a common source. By calling RMEMeas each mechanism that belongs to the same Origin is collected into a single larger, independent mechanism. By doing this, we see our uncertainties are dominated by the VNA drift, cable bend variations, connection repeatability, and the physical dimensions of our the primary standards used to define the calibration kit.

grouped_mag = mag.categorize_by('Origin')
grouped_phase = phase.categorize_by('Origin')
total_mag_variance = grouped_mag.stdunc().cov**2
total_phase_variance = grouped_phase.stdunc().cov**2
mag_variance = []
phase_variance = []
fig,axs = plt.subplots(2,1)
for um in grouped_mag.umech_id:
    mag_var_i = grouped_mag.usel(umech_id = [um]).stdunc().cov**2
    phase_var_i = grouped_phase.usel(umech_id = [um]).stdunc().cov**2
    mag_variance.append(mag_var_i/total_mag_variance*100)
    phase_variance.append(phase_var_i/total_phase_variance*100)

axs[0].stackplot(dut.nom['Frequency (GHz)'], mag_variance, labels = grouped_mag.umech_id)
axs[1].stackplot(dut.nom['Frequency (GHz)'], mag_variance, labels = grouped_phase.umech_id)

handles, labels = axs[0].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper center', ncols = 3)

axs[1].set_xlabel('Frequency (GHz)')
axs[0].set_ylabel('Mag (% of Variation)')
axs[1].set_ylabel('Phase (% of Variation)')

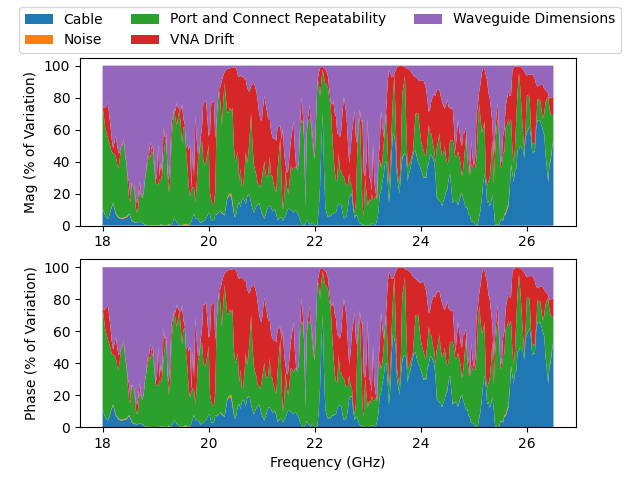
Text(38.347222222222214, 0.5, 'Phase (% of Variation)')