Solvers¶
FiPy requires either PETSc, pyamgx, SciPy, or Trilinos solver suites to be installed in order to solve linear systems. PETSc and Trilinos are the most complete of the solvers due to their numerous preconditioning and solver capabilities and they also allow FiPy to run in parallel. The Python interface for PETSc is better maintained than for Trilinos and tends to be easier to install. The sparse linear algebra solvers from the popular SciPy package are widely available and easy to install. Although they do not perform as well as the other suites and lack many of the features of PETSc or Trilinos, they may be the easiest linear solver choice when first installing and testing FiPy. pyamgx offers the possibility of solving sparse linear systems on the GPU; be aware that both hardware and software configuration is non-trivial. The Pysparse solver suite is no longer supported, as it requires Python 2.7; if you need Pysparse, please use FiPy 3.99.
FiPy chooses the solver suite based on system availability or based
on the user supplied Command-line Flags and Environment Variables. For example,
passing --trilinos:
$ python -c "from fipy import *; print DefaultSolver" --trilinos
<class 'fipy.solvers.trilinos.linearGMRESSolver.LinearGMRESSolver'>
uses a Trilinos solver. Setting FIPY_SOLVERS
to scipy:
$ FIPY_SOLVERS=scipy
$ python -c "from fipy import *; print DefaultSolver"
<class 'fipy.solvers.scipy.linearLUSolver.LinearLUSolver'>
uses a SciPy solver. Suite-specific solver classes can also be imported and instantiated overriding any other directives. For example:
$ python -c "from fipy.solvers.scipy import DefaultSolver; \
> print DefaultSolver" --trilinos
<class 'fipy.solvers.scipy.linearLUSolver.LinearLUSolver'>
uses a SciPy solver regardless of the command line argument.
Note
FiPy has not been designed to mix different solver suites during a given problem run
In the absence of Command-line Flags and Environment Variables, FiPy’s order of precedence when choosing the solver suite for generic solvers is PETSc followed by Trilinos, SciPy, and pyamgx.
|
|
|
|
||
solvers |
✓ |
✓ |
✓ |
✓ |
|
preconditioners |
✓ |
✓ |
✓ |
✓ |
✓ |
parallel |
✓ |
✓ |
|||
✓ |
✓ |
✓ |
✓ |
✓ |
|
✓ |
✓ |
✓ |
✓ |
||
✓ |
✓ |
||||
requirements |
|
PETSc¶
PETSc (the Portable, Extensible Toolkit for Scientific Computation) is a suite of data structures and routines for the scalable (parallel) solution of scientific applications modeled by partial differential equations. It employs the MPI standard for all message-passing communication (see Solving in Parallel for more details).
PyAMG¶
The PyAMG package provides adaptive multigrid preconditioners that can be used in conjunction with the SciPy solvers. While PyAMG also has solvers, they are not currently implemented in FiPy.
pyamgx¶
https://pyamgx.readthedocs.io/
The pyamgx package is a Python interface to the NVIDIA AMGX library. pyamgx can be used to construct complex solvers and preconditioners to solve sparse sparse linear systems on the GPU.
SciPy¶
https://docs.scipy.org/doc/scipy/reference/sparse.html
The scipy.sparse module provides a basic set of serial Krylov
solvers and a limited collection of preconditioners.
Trilinos¶
Trilinos provides a complete set of sparse matrices, solvers, and preconditioners. Trilinos preconditioning allows for iterative solutions to some difficult problems, and it enables parallel execution of FiPy (see Solving in Parallel for more details).
Performance Comparison¶
Comparing different solver suites, or even different solvers, has historically been difficult. The different suites have different interpretations of Convergence and tolerance. FiPy 4.0 harmonizes the different suites so that, to the greatest extent possible, all interpret Convergence and tolerance the same way. In the course of doing this, a number of inefficiencies were found in the way that FiPy built sparse matrices. To see the impact of these changes, we examine the serial and parallel scaling performance of the different solver suites for two different benchmark problems.
Note
Although the legacy Pysparse solver suite is no longer supported, its performance is included here for reference.
Serial Performance¶
Serial performance is compared for the different suites.
The following plot shows the serial scaling behavior for the different solvers. We compare solution time vs number mesh cells for a diffusion problem.
(Source code, png, hires.png, pdf)
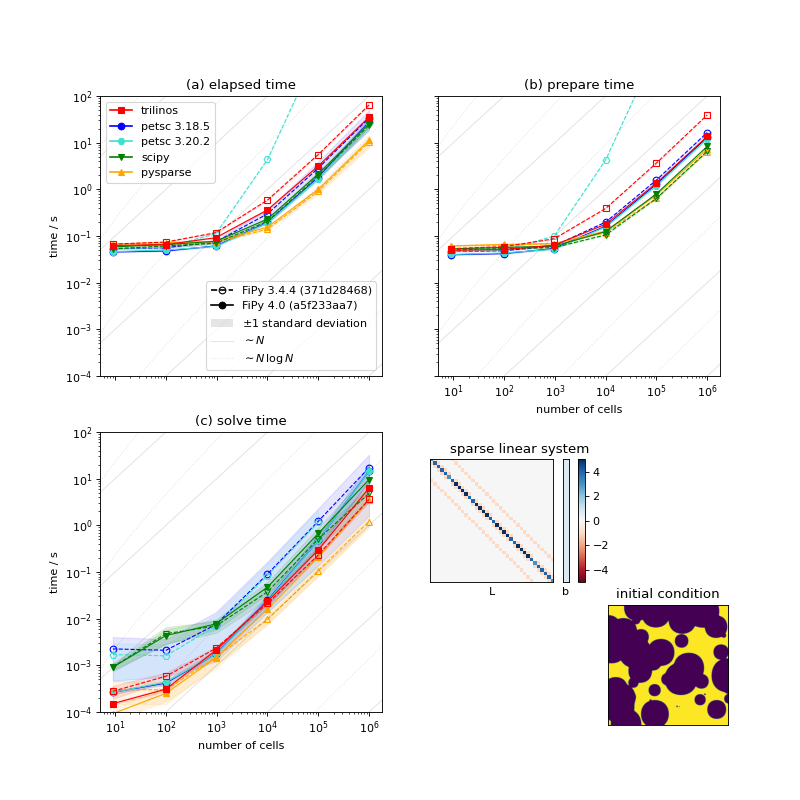
Comparison of serial performance for different solver suites, solvers and preconditioners, and different versions of FiPy [4]. (a) Total elapsed time, (b) time to prepare the matrix, and (c) time to solve the matrix as functions of mesh size. [5]¶
We can see:
For sufficiently large problems, building the matrix can be expected to scale as the number of cells \(N\) and solving the matrix should scale as \(N\,\ln N\). There are not enough data points to differentiate these slopes.
Below about 1000 cells, the time to prepare the matrix is insensitive to mesh size and this dominates the overall elapsed time.
There is nearly three orders of magnitude between the fastest solver/preconditioner and the slowest. This particular problem is not especially sensitive to choice of solver and preconditioner, as preparing the matrix takes the majority of the overall time, but it can be worth optimizing the choice for more complex systems of equations.
Matrix preparation time is terrible when older FiPy is combined with newer PETSc. PETSc 3.19 introduced changes to “provide reasonable performance when no preallocation information is provided”. Our experience is opposite that; FiPy did not supply preallocation information prior to version 4.0, but matrix preparation performance was fine with older PETSc releases. FiPy 4.0 does supply preallocation information and matrix preparation time is comparable for all tested versions of PETSc.
There is considerable dispersion about the mean solve time for different solvers and preconditioners. On the other hand, the time to prepare the matrix is insensitive to the choice of solver and preconditioner and shows a high degree of consistency from run to run.
(Source code, png, hires.png, pdf)
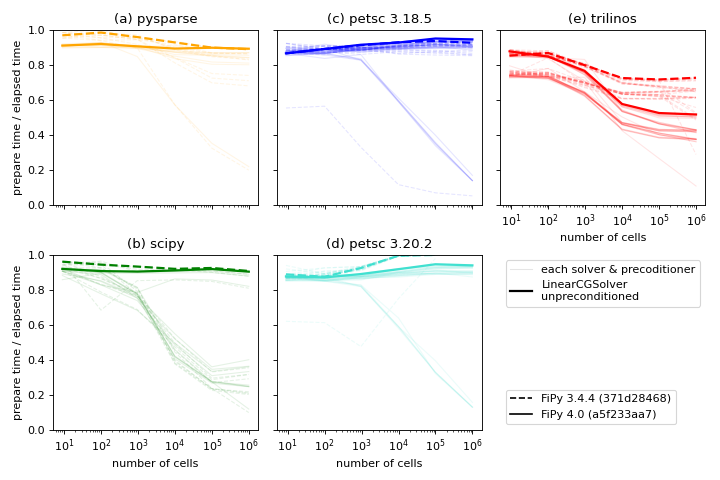
Ratio of time to prepare the matrix to the combined time to prepare and
solve the matrix for different solver suites, solvers
and preconditioners, and different versions of FiPy
[4] [5]. The thick lines highlight LinearCGSolver
with no preconditioner, one of the better-performing combinations
available in all suites.¶
In principle, we’d like to spend as little time preparing the matrix,
relative to solving it, as possible. This metric can be deceptive. If we
compare the case of unpreconditioned LinearCGSolver, one of the fastest
combinations for all suites for this problem, we see that Trilinos
has the lowest ratio of prepare to elapsed time. Examination of elapsed
time, the quantity we really care about, shows that Trilinos takes
three times as long to both prepare and solve as Pysparse or
SciPy and twice as long as PETSc.
For your own work, focus on identifying the solver and preconditioner with the lowest overall time to build and solve; this will counterintuitively have the highest ratio of prepare-to-elapsed time. Prepare time to elapsed time is a more useful metric for the FiPy developers; just as FiPy 4.0 brought considerable reductions in matrix build time, we will continue to seek opportunities to optimize.
Parallel Performance¶
The following plot shows the scaling behavior for multiple processors. We compare solution time vs number of Slurm tasks (available cores) for a Method of Manufactured Solutions Allen-Cahn problem.
(Source code, png, hires.png, pdf)
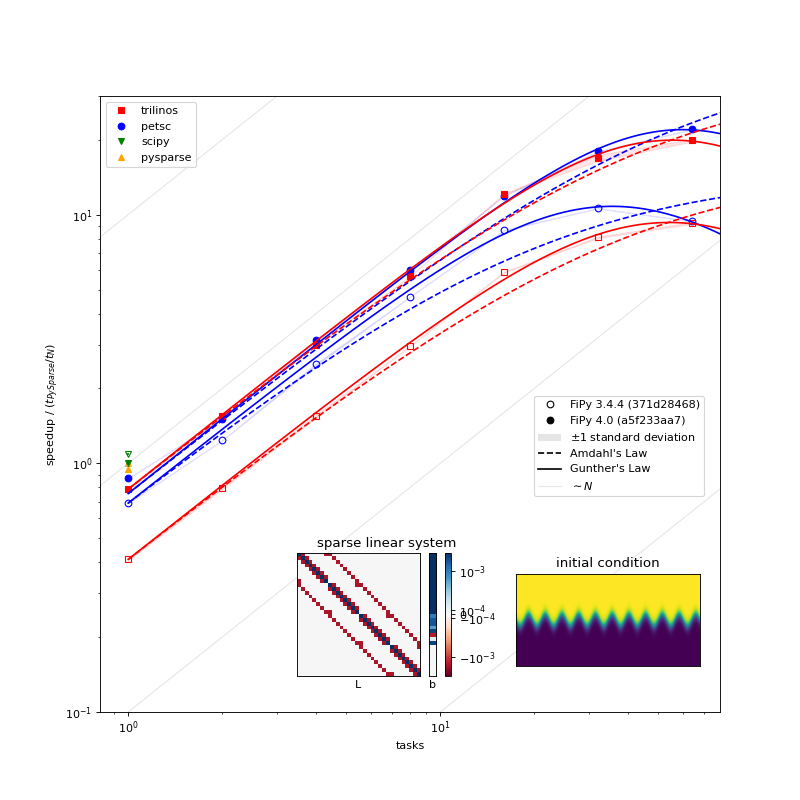
Parallel scaling behavior of different solver packages and different versions of FiPy [4] [6].¶
A few things can be observed in this plot:
PETSc, Pysparse, Trilinos, and SciPy have comparable serial performance, with SciPy edging out the other three for this particular problem.
FiPy 4.0 is roughly the same speed in serial, but more than twice as fast in parallel compared to FiPy 3.4.4 when using the PETSc solvers. FiPy 4.0 is roughly twice as fast using the Trilinos solvers, whether in serial or parallel.
FiPy 4.0 exhibits better parallel scaling than FiPy 3.4.4. Amdahl’s Law, \(\text{speedup} = p / (1 + \sigma(p - 1))\), does not fit the performance data nearly as well as Gunther’s Law, \(\text{speedup} = p / (1 + \sigma(p - 1) + \kappa p (p-1))\), where \(p\) is the number of parallel tasks, \(\sigma\) is the fraction limited by serial processes, and \(\kappa\) is “coherency” (which is somewhat nebulous).
Parallel scaling fitting parameters (smaller numbers are better)¶ Amdahl
Gunther
serial / %
serial / %
coherency
FiPy 3.4.4
petsc
4.7(3)
0.91(9)
0.00078(2)
trilinos
2.6(1)
0.8(1)
0.00034(2)
FiPy 4.0
petsc
1.70(8)
0.13(7)
0.00028(1)
trilinos
2.2(1)
0.4(1)
0.00032(3)
At least one source of less-than-optimal scaling is that our
“...Grid...” meshes parallelize by dividing the mesh into slabs, which
leads to more communication overhead than more compact partitions. The
“...Gmsh...” meshes partition more efficiently, but carry more overhead
in other ways. We’ll be making efforts to improve the partitioning of the
“...Grid...” meshes in a future release.
These results are likely both problem and architecture dependent. You should develop an understanding of the scaling behavior of your own codes before doing “production” runs.
FiPy version 3.4.4 has different interpretations of Convergence for different solver suites (and even for different solvers). Benchmarks used a patched version (371d28468) that provided more logging information and normalized interpretation of tolerance, but without any of the improvements in matrix and solver efficiency of version 4.0.
Calculations are of diffusion of a binary alloy in a frozen
two-phase field. Solutions are on a square
Grid2D. The initial condition is sampled
from the center of a well-evolved \(1024\times 1024\)
nucleation simulation.
All available solvers and
preconditioners are attempted. Solution tolerance is 1e-10 using
the "RHS" convergence criterion. Simulations
were run on an AMD Epyc 7702 CPU with 64 cores featuring two-thread
Simultaneous Multi-Threading (SMT) and 512 GB of memory.
OMP_NUM_THREADS was set to 1.
Calculations are of a
Method of Manufactured Solutions Allen-Cahn problem. Solutions are
on a \(2048\times 1024\) Grid2D
and the LinearCGSolver with no preconditioner is used for
all solver suites. Solution tolerance is 1e-10 using the "RHS"
convergence criterion. Five replicates of each
simulation were run on an AMD Epyc 7702 CPU with 64 cores featuring
two-thread Simultaneous Multi-Threading (SMT) and 512 GB of memory.
OMP_NUM_THREADS was set to 1.
Convergence¶
Different solver suites take different approaches to testing convergence.
We endeavor to harmonize this behavior by allowing the strings in the
“criterion” column to be passed as an argument when instantiating a
Solver. Convergence is detected if
residual < tolerance * scale.
criterion |
residual |
scale |
||||
|---|---|---|---|---|---|---|
|
\(\|\mathsf{L}\vec{x} - \vec{b}\|_2\) |
\(1\) |
|
|
||
|
\(\|\mathsf{L}\vec{x} - \vec{b}\|_2\) |
\(\|\vec{b}\|_2\) |
|
|
||
|
\(\|\mathsf{L}\vec{x} - \vec{b}\|_2\) |
\(\|\mathsf{L}\|_\infty\) |
|
|||
|
\(\|\mathsf{L}\vec{x} - \vec{b}\|_2\) |
\(\|\mathsf{L}\vec{x} - \vec{b}\|_2^{(0)}\) |
|
|
||
|
\(\|\mathsf{L}\vec{x} - \vec{b}\|_\infty\) |
\(\|\mathsf{L}\|_\infty * \|\vec{x}\|_1 + \|\vec{b}\|_\infty\) |
|
|||
|
\(\left\|\mathsf{P}^{-1}(\mathsf{L}\vec{x} - \vec{b})\right\|_2\) |
\(\left\|\vec{b}\right\|_2\) |
||||
|
\(\sqrt{(\mathsf{L}\vec{x} - \vec{b})\mathsf{P}^{-1}(\mathsf{L}\vec{x} - \vec{b})}\) |
\(\left\|\vec{b}\right\|_2\) |
||||
|
|
|
|
|
||
|
|
|
|
|
Note
PyAMG is a set of preconditioners applied on top of SciPy, so is not explicitly included in these tables.
Tolerance¶
The default tolerance is \(10^{-5}\) (the legacy tolerance, prior to FiPy 4.0, was \(10^{-10}\)).
default¶
The setting criterion="default" applies the same scaling (RHS) to
all solvers. This behavior is new in FiPy 4.0; prior to that, the
default behavior was the same as criterion="legacy".
legacy¶
The setting criterion="legacy" restores the behavior of FiPy
prior to version 4.0 and is equivalent to what the particular suite and solver
does if not specifically configured. The legacy row of the table is a
best effort at documenting what will happen.
Note
All LU solvers use
"initial"scaling.PETSc accepts
KSP_NORM_DEFAULTin order to “use the default for the currentKSPType”. Discerning the actual behavior would require burning the code in a bowl of chicken entrails. (It is reasonable to assumeKSP_NORM_PRECONDITIONEDfor left-preconditioned solvers andKSP_NORM_UNPRECONDITIONEDotherwise.)Even the PETSc documentation says that
KSP_NORM_NATURALis “weird”).
absolute_tolerance¶
PETSc and SciPy Krylov solvers accept an additional
absolute_tolerance parameter, such that convergence is detected if
residual < max(tolerance * scale, absolute_tolerance).
divergence_tolerance¶
PETSc Krylov solvers accept a third divergence_tolerance parameter,
such that a divergence is detected if residual > divergence_tolerance *
scale. Because of the way the convergence test is coded,
if the initial residual is much larger than the norm of the right-hand-side
vector, PETSc will abort with KSP_DIVERGED_DTOL without ever trying to
solve. If this occurs, either divergence_tolerance should be increased
or another convergence criterion should be used.
Note
See examples.diffusion.mesh1D,
examples.diffusion.steadyState.mesh1D.inputPeriodic,
examples.elphf.diffusion.mesh1D,
examples.elphf.phaseDiffusion, examples.phase.binary,
examples.phase.quaternary, and
examples.reactiveWetting.liquidVapor1D for several examples where
criterion="initial" is used to address this situation.
Note
divergence_tolerance never caused a problem in previous versions of
FiPy because the default behavior of PETSc is to zero out the
initial guess before trying to solve and then never do a test against
divergence_tolerance. This resulted in behavior (number of
iterations and ultimate residual) that was very different from the other
solver suites and so FiPy now directs PETSc to use the initial
guess.
Reporting¶
Different solver suites also report different levels of detail about why
they succeed or fail. This information is captured as a
Convergence or
Divergence property of the
Solver after calling
solve() or
sweep().
Convergence criteria met. |
|||||
Requested iterations complete (and no residual calculated). |
|||||
Converged, residual is as small as seems reasonable on this machine. |
|||||
Converged, \(\mathbf{b} = 0\), so the exact solution is \(\mathbf{x} = 0\). |
|||||
Converged, relative error appears to be less than tolerance. |
|||||
“Exact” solution found and more iterations will just make things worse. |
|||||
The iterative solver has terminated due to a lack of accuracy in the recursive residual (caused by rounding errors). |
|||||
Solve still in progress. |
Illegal input or the iterative solver has broken down. |
|||||
Maximum number of iterations was reached. |
|||||
The system involving the preconditioner was ill-conditioned. |
|||||
An inner product of the form \(\mathbf{x}^T \mathsf{P}^{-1} \mathbf{x}\) was not positive, so the preconditioning matrix \(\mathsf{P}\) does not appear to be positive definite. |
|||||
The matrix \(\mathsf{L}\) appears to be ill-conditioned. |
|||||
The method stagnated. |
|||||
A scalar quantity became too small or too large to continue computing. |
|||||
Breakdown when solving the Hessenberg system within GMRES. |
|||||
The residual norm increased by a factor of |
https://petsc.org/release/docs/manual/ksp/#sec-convergencetests
AMGX REFERENCE MANUAL: 2.3 General Settings: convergence,
October 2017, API Version 2,
https://github.com/NVIDIA/AMGX/blob/main/doc/AMGX_Reference.pdf
AztecOO Users Guide: 3.1 Aztec Options: options[AZ_conv],
SAND REPORT SAND2004-3796, Updated August 2007,
For AztecOO Version 3.6 in Trilinos Release 8.0,
https://trilinos.github.io/pdfs/AztecOOUserGuide.pdf
Implemented by FiPy using intrinsic solver capabilities.
 FiPy
FiPy