Multi-fluid Parameter Fitting

Here is an example of fitting the \(\beta_T\) and \(\gamma_T\) values for the binary pair of propane+\(n\)-dodecane with the multi-fluid model. It uses differential evolution to do the global optimization, which is probably overkill in this case as the problem is 2D and other algorithms like Nelder-Mead or even approximate Hessian methods would probably be fine.

In any case, it takes a few seconds to run (when the actual optimization is uncommented), demonstrating how one can fit model parameters with existing tooling from the scientific python stack.

import json
import teqp, numpy as np, pandas, matplotlib.pyplot as plt
import scipy.interpolate, scipy.optimize

import pandas
data = pandas.read_csv('VLE_data_propane_dodecane.csv')

def cost_function(parameters:np.ndarray, plot:bool=False):

    # Fitting some parameters and fixing the others
    betaV, gammaV = 1.0, 1.0
    betaT, gammaT = parameters

    # betaT, gammaT, betaV, gammaV = parameters

    BIP = [{
        'function': '',
        'BibTeX': 'thiswork',
        'CAS1': '112-40-3',
        'CAS2': '74-98-6',
        'F': 0.0,
        'Name1': 'n-Dodecane',
        'Name2': 'n-Propane',
        'betaT': betaT,
        'betaV': betaV,
        'gammaT': gammaT,
        'gammaV': gammaV
    }]
    model = teqp.build_multifluid_model(["n-Dodecane", "n-Propane"], teqp.get_datapath(),
        BIPcollectionpath=json.dumps(BIP)
    )
    ancs = [model.build_ancillaries(ipure) for ipure in [0,1]]

    cost = 0.0

    # The 0-based index of the fluid to start from. At this temperature, only one fluid
    # is subcritical, so it has to be that one, but in general you could start
    # from either one.
    ipure = 0

    for T in [419.15, 457.65]:
        # Subset the experimental data to match the isotherm
        # being fitted
        dfT = data[np.abs(data['T / K90'] - T) < 1e-3]

        if plot:
            plt.plot(1-dfT['x[0] / mole frac.'], dfT['p / Pa']/1e6, 'X')
            plt.plot(1-dfT['y[0] / mole frac.'], dfT['p / Pa']/1e6, 'X')

        try:
            # Get the molar concentrations of the pure fluid
            # at the starting point
            anc = ancs[ipure]
            rhoL0 = np.array([0, 0.0])
            rhoV0 = np.array([0, 0.0])
            rhoL0[ipure] = anc.rhoL(T)
            rhoV0[ipure] = anc.rhoV(T)

            # Now we do the trace and convert retuned JSON
            # data into a DataFrame
            df = pandas.DataFrame(model.trace_VLE_isotherm_binary(T, rhoL0, rhoV0))

            if plot:
                plt.plot(df['xL_0 / mole frac.'], df['pL / Pa']/1e6)
                plt.plot(df['xV_0 / mole frac.'], df['pL / Pa']/1e6)

            # Interpolate trace at experimental pressures along this
            # isotherm to get composition from the current model
            # The interpolators are set up to put in NaN for out
            # of range values
            x_interpolator = scipy.interpolate.interp1d(
                df['pL / Pa'], df['xL_0 / mole frac.'],
                fill_value=np.nan, bounds_error=False
            )
            y_interpolator = scipy.interpolate.interp1d(
                df['pL / Pa'], df['xV_0 / mole frac.'],
                fill_value=np.nan, bounds_error=False
            )
            # The interpolated values for the compositions
            # along the trace at experimental pressures
            x_model = x_interpolator(dfT['p / Pa'])
            y_model = y_interpolator(dfT['p / Pa'])
            if plot:
                plt.plot(x_model, dfT['p / Pa']/1e6, '.')

            # print(x_model, (1-dfT['x[0] (-)']))

            errTx = np.sum(np.abs(x_model-(1-dfT['x[0] / mole frac.'])))
            errTy = np.sum(np.abs(y_model-(1-dfT['y[0] / mole frac.'])))

            # If any point *cannot* be interpolated, throw out the model,
            # returning a large cost function value.
            #
            # Note: you might need to be more careful here,
            # if the points are close to the critical point, a good model might
            # (but not usually), undershoot the critical point of the
            # real mixture
            #
            # Also watch out for values of compositons in the data that are placeholders
            # with a value of nan, which will pollute the error calculation
            if not np.isfinite(errTx):
                return 1e6
            if not np.isfinite(errTy):
                return 1e6
            cost += errTx + errTy

        except BaseException as BE:
            print(BE)
            pass
    if plot:
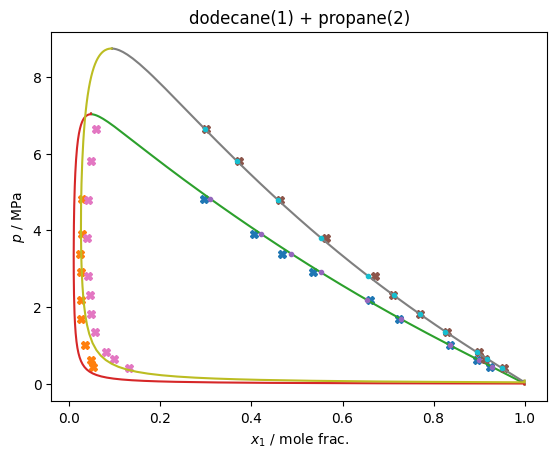
        plt.title(f'dodecane(1) + propane(2)')
        plt.xlabel('$x_1$ / mole frac.'); plt.ylabel('$p$ / MPa')
        plt.savefig('n-Dodecane+propane.pdf')
        plt.show()

    return cost

# The final parameter values, will be overwritten if
# optimization call is uncommented
x = [1.01778992, 1.17318854]

# Here is the code used to do the optimization, uncomment to run it
# Note: it is commented out because it takes too long to run on doc builder
#
# res = scipy.optimize.differential_evolution(
#     cost_function,
#     bounds=((0.9, 1.5), (0.75, 1.5)),
#     disp=True,
#     polish=False
# )
# print(res)
# x = res.x

cost_function(x, plot=True)

np.float64(0.47041664919729653)