VLLE

Following the approach described in Bell et al.: https://doi.org/10.1021/acs.iecr.1c04703

for the mixture of nitrogen + ethane, with the default thermodynamic model in teqp, which is the GERG-2008 mixing parameters (no departure function).

Two traces are made, and the intersection is obtained, this gives you the VLLE solution.

import teqp, numpy as np, matplotlib.pyplot as plt, pandas

def get_traces(*, T, ipures):
    names = ['Nitrogen', 'Ethane']
    model = teqp.build_multifluid_model(names, teqp.get_datapath())
    pures = [teqp.build_multifluid_model([name], teqp.get_datapath()) for name in names]
    traces = []
    for ipure in ipures:
        # Init at the pure fluid endpoint
        anc = pures[ipure].build_ancillaries()
        rhoLpure, rhoVpure = pures[ipure].pure_VLE_T(T, anc.rhoL(T), anc.rhoV(T), 10)

        rhovecL = np.array([0.0, 0.0])
        rhovecV = np.array([0.0, 0.0])
        rhovecL[ipure] = rhoLpure
        rhovecV[ipure] = rhoVpure
        opt = teqp.TVLEOptions()
        opt.p_termination = 1e8
        opt.crit_termination=1e-4
        opt.calc_criticality=True
        j = model.trace_VLE_isotherm_binary(T, rhovecL, rhovecV, opt)
        traces.append(j)
    return model, traces

T = 120.3420
model, traces = get_traces(T=T, ipures=[0,1])
for trace in traces:
    df = pandas.DataFrame(trace)
    plt.plot(df['xL_0 / mole frac.'], df['pL / Pa'])
    plt.plot(df['xV_0 / mole frac.'], df['pV / Pa'])

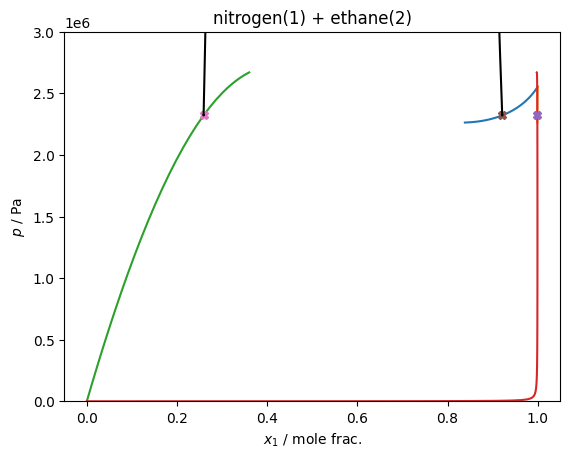
# Do the VLLE solving
for soln in model.find_VLLE_T_binary(traces):
    print('rhovec / mol/m^3 | p / Pa')
    for rhovec in soln['polished']:
        rhovec = np.array(rhovec)
        rhotot = sum(rhovec)
        x = rhovec/rhotot
        p = rhotot*model.get_R(x)*T*(1+model.get_Ar01(T, rhotot, x))
        plt.plot(x[0], p, 'X')
        print(rhovec, p)

    # And also carry out the LLE trace for the two liquid phases
    j = model.trace_VLE_isotherm_binary(T, np.array(soln['polished'][1]), np.array(soln['polished'][2]))
    df = pandas.DataFrame(j)
    plt.plot(df['xL_0 / mole frac.'], df['pL / Pa'], 'k')
    plt.plot(df['xV_0 / mole frac.'], df['pV / Pa'], 'k')

# Plotting niceties
plt.ylim(top=3e6, bottom=0)
plt.gca().set(xlabel='$x_1$ / mole frac.', ylabel='$p$ / Pa', title='nitrogen(1) + ethane(2)')
plt.show()

rhovec / mol/m^3 | p / Pa
[3.66984834e+03 3.25893958e+00] 2321103.0873191245
[19890.16767481  1698.86505766] 2321103.0873192116
[ 5641.24690517 16140.85769908] 2321103.087318882

T = 113.0
model, traces = get_traces(T=T, ipures = [0,1])

# Find the VLLE solution for the starting temperature
solns = model.find_VLLE_T_binary(traces)
rhovecV, rhovecL1, rhovecL2 = solns[0]['polished']

# Trace towards lower and higher temperatures
for init_dT in [1.0e-3, -1.0e-3]:

    opt = teqp.VLLETracerOptions()
    opt.init_dT = init_dT
    opt.T_limit = -1 if init_dT < 0 else 10000
    opt.verbosity = 100
    a = lambda x: np.array(x)
    VLLE = model.trace_VLLE_binary(T, a(rhovecV), a(rhovecL1), a(rhovecL2), opt)
    df = pandas.DataFrame(VLLE)
    if df.empty:
        raise ValueError('No results')

    # Add the pressure to the DataFrame
    def add_ps(row, key):
        T = row['T / K']
        rhovec = np.array(row[key])
        rhotot = sum(rhovec)
        x = rhovec/rhotot
        p = rhotot*model.get_R(x)*T*(1+model.get_Ar01(T, rhotot, x))
        return p
    df['p / Pa']  = df.apply(add_ps, axis=1, key='rhoV / mol/m^3')

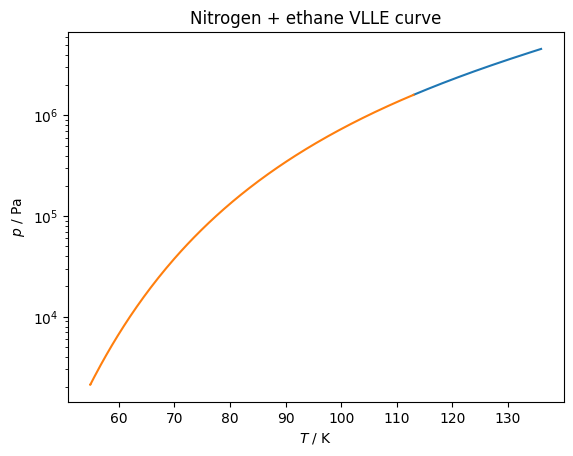
    # Plot the p-T curve
    plt.plot(df['T / K'], df['p / Pa'])

plt.gca().set(xlabel='$T$ / K', ylabel='$p$ / Pa', yscale='log')
plt.title('Nitrogen + ethane VLLE curve')

Calculated pressure is not finite

Text(0.5, 1.0, 'Nitrogen + ethane VLLE curve')