# Problem Set-Up
Larry Aagesen ([@laagesen](https://github.com/laagesen)),
David Montiel,
Sourabh Kadambi ([@sourabhkadambi](https://github.com/sourabhkadambi)),
Sudipta Biswas ([@SudiptaBiswas](https://github.com/SudiptaBiswas))
After the phase-field model formulation is developed, implemented in code, and
verified, it can be set up to solve the scientific/engineering problem of
interest. The purpose of this page is to give guidance on some of the important
considerations when setting up your code to solve your specific problem,
organized in the following sections:
[Spatial dimension (1D vs. 2D vs. 3D)](#spatial-dimension)
[Initial conditions](#initial-conditions)
[Boundary conditions](#boundary-conditions)
[Interface width](#interface-width)
[Convergence](#convergence-studies)
[Impact of orientation](#impact-of-orientation)
[Kinetics and how long to run](#kinetics-and-how-long-to-run)
## Spatial Dimension
In setting up a phase-field simulation, it is important to understand the role
of spatial dimensions in the physics governing the problem, and how that might
impact the simulation results and its interpretation. This is particularly
important if simulations are being performed in reduced dimensions compared to
the actual dimension of the problem, which is a common practice employed to
reduce the computational costs.
It is likely that the physical behavior of a certain phenomenon might scale
differently in 1D, 2D and 3D. This could be related to the physical processes
in the bulk regions of the system or at the interfacial regions or both. For
instance, the amount of interfacial region relative to the bulk phase region
differs in 1D, 2D and 3D, and also governs many physical aspects of material
behavior.
Therefore, it is important to determine how reduced dimensionality might affect
predictions or comparison of simulation results with reality. In certain
situations, on the other hand, it might be appropriate to setup the problem in
reduced dimensions of 1D or 2D due to the inherent symmetry or directionality
in the problem. Moreover, for simple microstructure geometries, it might be
possible to setup the model in cylindrical or spherical coordinates, which can
allow the simplicity of 1D computations while also capturing 2D and 3D behavior
of the model accurately.
### Example
To demonstrate a case where simulation outcomes can significantly differ in
different dimensions, we consider the [single seed
case](https://pages.nist.gov/pfhub/benchmarks/benchmark8.ipynb/#Part-%28a%29)
of the [homogeneous
nucleation](https://www.sciencedirect.com/science/article/abs/pii/S0927025621000963?via%3Dihub)
benchmark problem. A simple phase-field model with a single non-conserved order
parameter describes an isothermal pure substance with one liquid phase (order
parameter = $0$) and one solid phase (order parameter = $1$). The nucleation
driving force for the solid phase is $\Delta f=\sqrt2/30$. The free energy of
the diffuse interface is $\gamma = 1/3\sqrt2$.
We consider a seed nucleus of $7.5$ unit radius in 2D and 3D. The 2D simulation
domain is of size $100\times100$, and the 3D simulation domain is of size $40
\times 40 \times 40$. The nucleus is centered at $x=y=z=0$. Uniform mesh of
element size $\Delta x = 0.09765$ is used. Neumann boundary conditions, given
by the zero normal-derivative of the order parameter, are applied on all domain
boundaries. The figure below shows the starting geometry of the nucleus in 2D
(left) and 3D (right).
 The time evolution of the order parameter, given by the Allen-Cahn equation,
was solved using the MOOSE framework. Details of the numerical method can be
found in [Wu _et al._ (2021)](
https://www.sciencedirect.com/science/article/abs/pii/S0927025621000963?via%3Dihub).
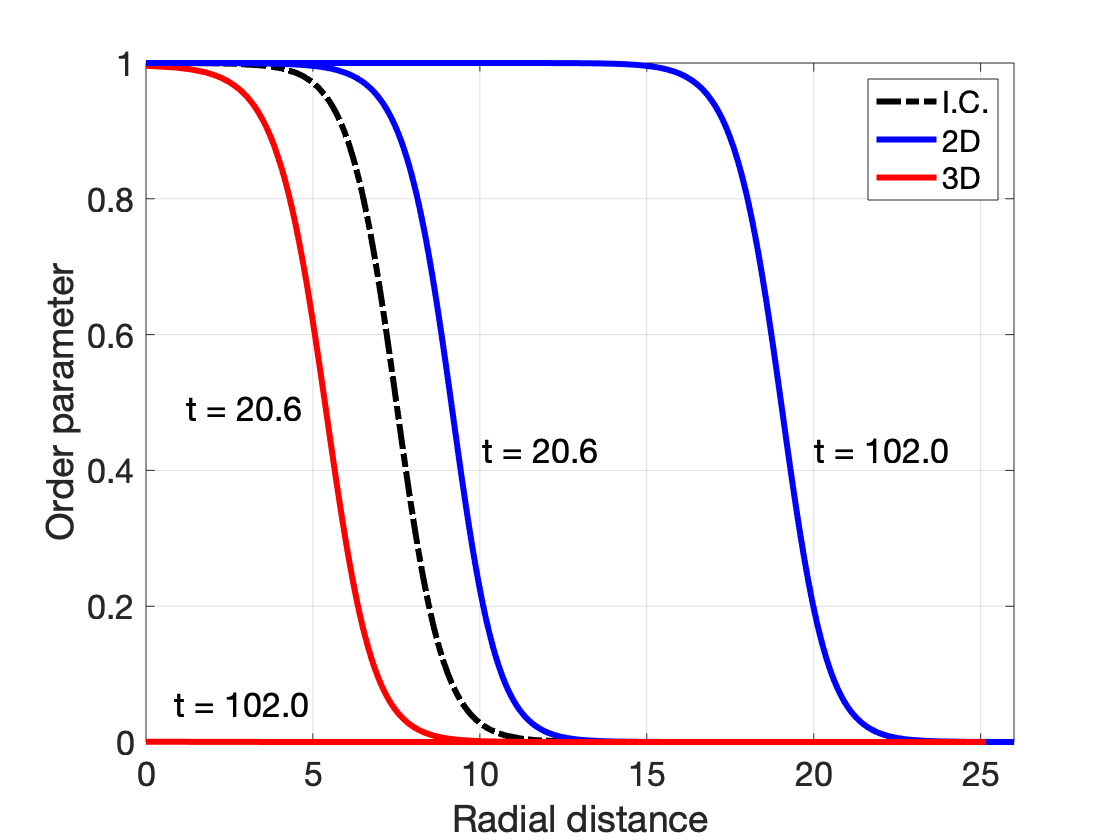
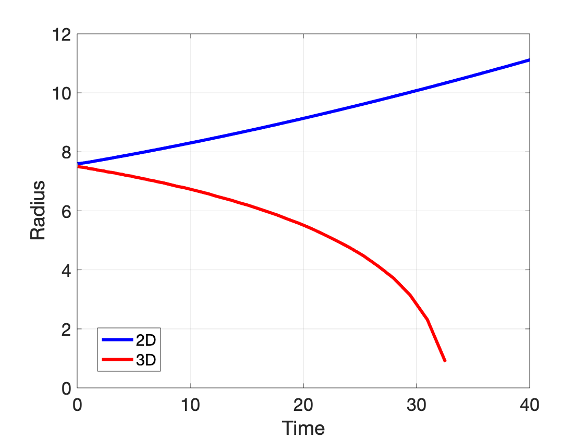
The simulations results of nucleus evolution are shown in the figures below:
(left) order parameter profile measured radially from the center of domain at
different evolution times; (right) radius as a function of evolution time. We
see that the seed of same starting radius $r_\circ = 7.5$ units evolves starkly
differently in 2D and 3D. While the nucleus grows in 2D, it shrinks and
dissolves in 3D.
The time evolution of the order parameter, given by the Allen-Cahn equation,
was solved using the MOOSE framework. Details of the numerical method can be
found in [Wu _et al._ (2021)](
https://www.sciencedirect.com/science/article/abs/pii/S0927025621000963?via%3Dihub).
The simulations results of nucleus evolution are shown in the figures below:
(left) order parameter profile measured radially from the center of domain at
different evolution times; (right) radius as a function of evolution time. We
see that the seed of same starting radius $r_\circ = 7.5$ units evolves starkly
differently in 2D and 3D. While the nucleus grows in 2D, it shrinks and
dissolves in 3D.
The role of dimensionality in homogeneous nucleation can be understood from the
classical nucleation theory where the solid-liquid interface is modeled as a
mathematically sharp interface. The interface is a 1D line in a 2D system and a
2D plane in a 3D system. The free energy of the nucleus particle $\Delta G(r)$
is a balance between the energy cost in forming the interface, and the energy
released due to the driving force in forming the bulk particle. For a 2D
system, $\Delta G(r) = 2\pi r\gamma - \pi r^2 \Delta f$. For a 3D system,
$\Delta G(r) = 4 \pi r^2 \gamma - (4 \pi /3) r^3 \Delta f$. When the rate of
change of free energy with respect to particle size is negative, the particle
is favored to grow; otherwise it will shrink and dissolve. By setting $d \Delta
G / d r = 0$, we obtain the critical radius as $r_c = \gamma/ \Delta f$ in 2D
and $r_c = 2\gamma/ \Delta f$ in 3D.
We can now apply the above sharp-interface analysis to our diffuse interface
approximation in the phase-field model. For the given model parameters, we
obtain $r_c = 5$ units in 2D and $r_c = 10$ units in 3D. In our simulation
setup of $r_\circ = 7.5$ units, $r_\circ$ $>$ $r_c$ in 2D, but $r_\circ < r_c$
in 3D. Therefore, the nucleus is favored to grow in 2D but shrinks in 3D as
observed in the simulations.
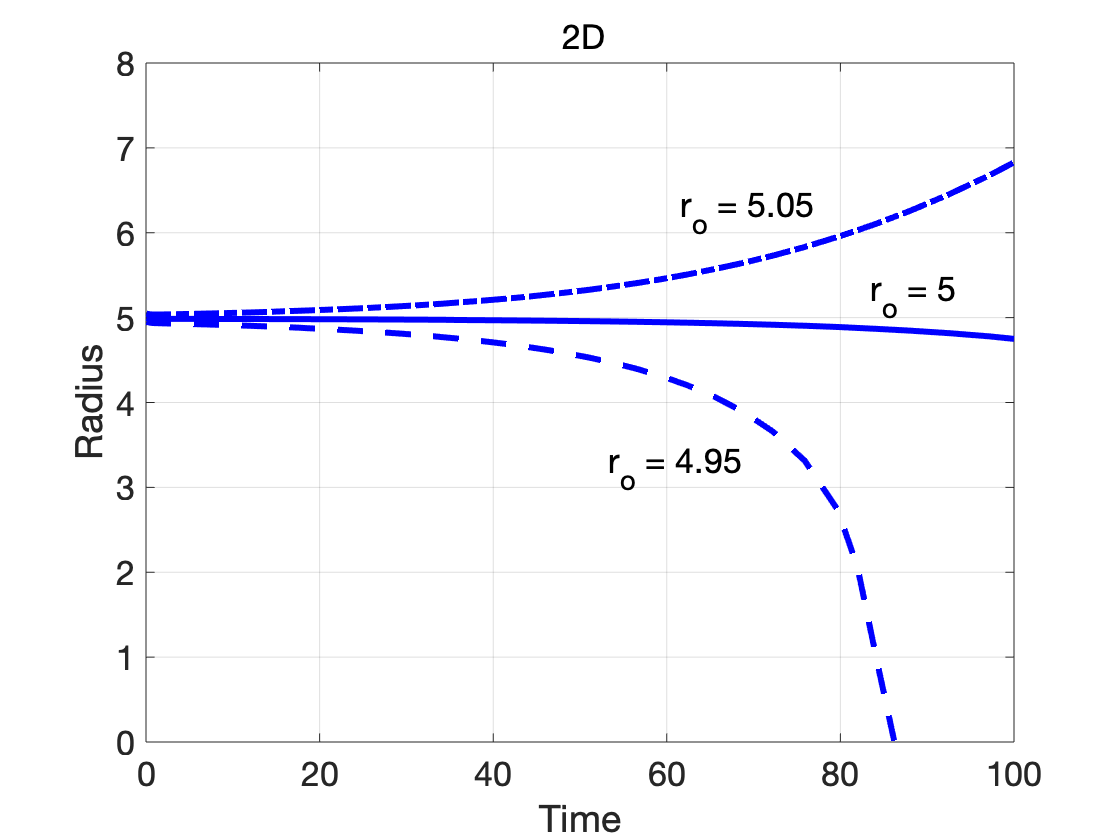
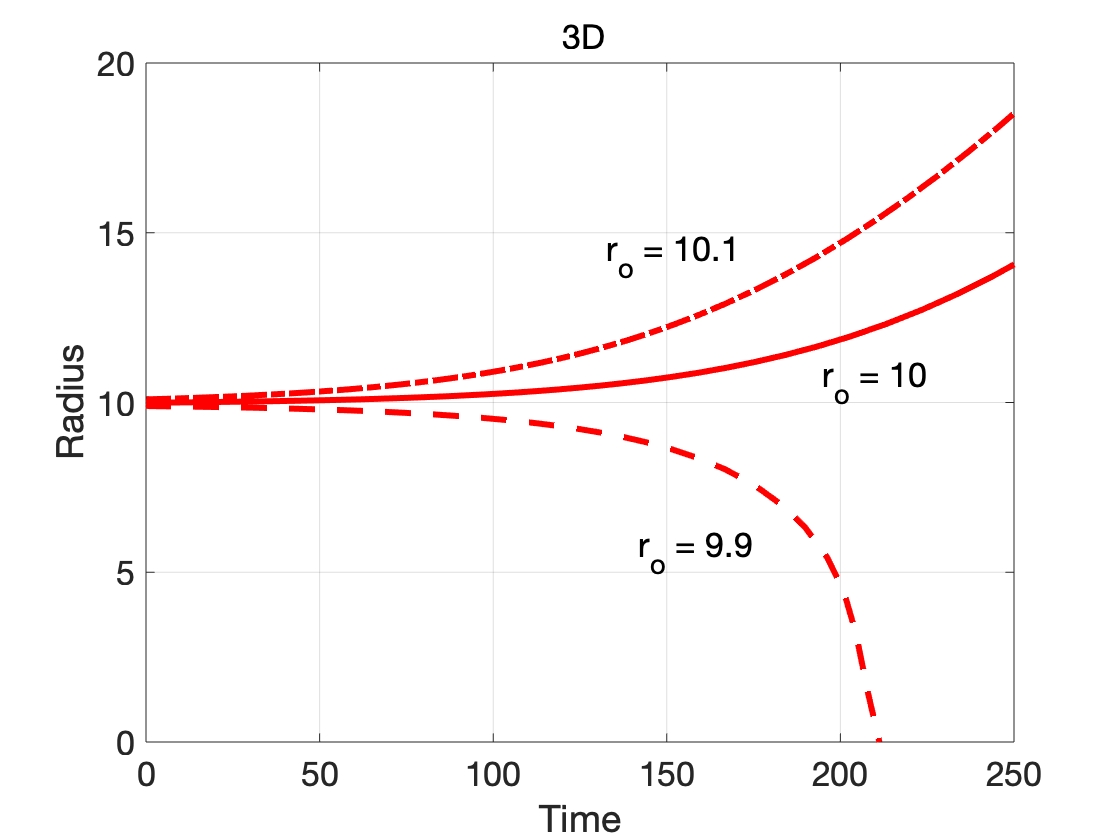 The dependence on dimensionality is further illustrated by considering cases
where the initial radius is close to the critical radius: $r_\circ = 0.99 r_c$,
$r_\circ = r_c$ and $r_\circ = 1.01 r_c$. The simulation results of radius
evolution are shown above for 2D (left) and 3D (right). As expected from the
the classical homogeneous nucleation theory, the sub-critical nucleus with
$r_\circ = 0.99 r_c$ shrinks and the super-critical nucleus with $r_\circ =
1.01 r_c$ grows.
Since the nucleus in the phase-field model is a diffuse-interface approximation
of the classical sharp interface nucleus, $r_\circ = r_c$ is fairly close to an
unstable equilibrium. Ideally, the radius would remain constant with
time. However, since the system is unstable, small numerical errors accumulate
with time, eventually leading to growth or shrinkage of the nucleus. During
initial time steps, the interface profile is expected to undergo some changes
from the starting profile due to equilibration. While the $tanh$ function is a
common choice for the initial condition of the interface, it is an exact
solution only for a planar interface, representative of a 1D scenario.
## Initial conditions
For simulations of the evolution of two or more phases, it is important to
anticipate the expected equilibrium state of the system given the initial
conditions. To do this, one needs the phase diagram as determined by the bulk
contribution of the free energy density.
For example, in simulating phase separation following spinodal decomposition,
it is common to define the initial state of the order parameter as a spatially
uniform field with an added small 'noisy' perturbation with small
amplitude. However, this order parameter must be within the spinodal region of
the phase diagram, i.e., the region where spontaneous decomposition leads to a
decrease in the free energy. Below we show two instances that demonstrate that
choosing different values for the baseline order parameter, $c_{0,\mathrm{base}}$, and
the same initial perturbation term, $\xi(\vec{r})$, for the initial conditions
of leads to different dynamics.


## Boundary conditions
Boundary conditions (BC) are required to solve for the governing equations in
all phase field simulations. In general, every field must have a defined BC at
every boundary of the system. The three most common types of boundary
conditions (BC) for phase field simulation are:
- Dirichlet BC: The value of a field is specified at the boundary. This type of
boundary condition is useful whenever we want to impose a value to an order
parameter or field at one or more boundaries. Some common examples include
setting a constant value for temperature to simulate a heat reservoir, or
setting a constant value for a solid/liquid order parameter to indicate a
fixed phase beyond the confines of the system.
- Neumann BC: The value of the spatial derivative of a field is specified at
the boundary. This type of boundary conditions is useful to specify fluxes of
fields at the boundary. For example, setting natural BC (a special case of
Neumann BC) for a field at the boundary enforces that the normal component of
gradient of that field is zero along that boundary. Therefore, if a flux for
that field is proportional to this gradient, natural BC is equivalent to
imposing zero flux at the boundary. This BC is convenient to ensure that the
field is conserved. In addition, natural BCs are useful to exploit known
symmetries in the morphology of domains: for example a spherical domain can
be simulated using a quarter (in 2D) or eighth of a system (in 3D) by placing
centering the sphere in a corner of the system and imposing natural BCs along
the boundaries that define the corner.
- Periodic BCs: The value of the field in a boundary with periodic BC matches
the value from the opposite boundary. These type of BCs are useful to
simulate periodic domains, but also to minimize boundary effects. since the
system does not interact with borders.
### Try different boundary conditions and check their impact
We used the results from Benchmark [Problem 1a](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(a)-Square-periodic)
and [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
to analyze the effect of boundary conditions. In addition, we solved for
Cahn-Hilliard dynamics under the same initial condition and simulation
parameters as problem 1 but using mixed boundary conditions, i.e., different
boundary conditions for each boundary. We compare the results for each case at
simulation time _t_ = 1000. The simulations were carried out in the PRISMS-PF
framework using a uniform square mesh with $N_x = N_y = 128$ linear elements
and a time step, $\Delta t$ = 0.005. The results are shown in the figure below.

As can be seen in the figure above, for periodic boundary boundaries the
$\alpha$ - $\beta$ domains are **continuous** on opposite sides of the
system. For no-flux boundaries, the $\alpha$ - $\beta$ interfaces are
**normal** to the boundary. For Dirichlet boundaries (bottom boundary of the
right panel), the value of _c_ is **fixed** along the boundary.
## Interface width
Phase-field modeling is a diffuse interface approach, meaning that interfaces
are represented by a smooth variation of one or more order parameters across
the interface. The width of the interface is a function of the model parameters
and the interface width is determined by model parameter choices. In some
cases, an analytical expression is available that relates interface width to
phase-field model parameters (such as free energy barrier height and gradient
energy coefficient, which also impact the interfacial energy). In other cases,
no analytical solution is available and the interface width must be
approximated or determined numerically based on parameter choices. Such details
are specific to the formulation being used.
Once the relationship between model parameters and interface width is
understood, an appropriate selection of interface width needs to be made (while
maintaining the correct interfacial energy for the system being studied). In
some cases, the interface width in the phase-field model can be chosen to match
the actual physical width of the interface being studied (such typically
sub-nanometer). However, resolving a physically realistic interface width
requires a sub-nanometer grid/mesh (grid/mesh convergence is described further
in the next section). Using a physically realistic interface width often makes
it computationally unfeasible to simulate systems large enough to be
statistically representative. Therefore, in many cases an interfacial width
that is much larger than the the physical width of an interface is used. In
these cases, a careful balance between computational efficiency and model
accuracy is needed; the interface width should be chosen to be small enough
that the physics of the system are accurately represented, while maintaining
adequate computational performance. A useful rule of thumb as a starting point
is that the interface width should be at least an order of magnitude smaller
than the smallest microstructural feature size of interest. Starting from this
guideline, simulations of microstructural evolution with varying interface
widths can be run to ensure that the choice of interface width does not affect
the simulation results. A small test problem may be useful for testing
convergence with respect to interface width; for example a shrinking circular
grain embedded in another grain may be used for testing convergence of a grain
growth model with respect to interface width, rather starting with large,
costly simulations of hundreds of grains.
## Convergence studies
### Carry out grid/mesh convergence study AFTER you have finalized your interfacial width.
As an example of a mesh convergence study, we can consider [Benchmark Problem
1](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/) from the
Phase-Field Community Hub. In this problem, which models spinodal decomposition
using the Cahn-Hilliard equation, the width of the diffuse interface is 4.47,
as defined by the Cahn-Hilliard equation and physical parameters in the problem
statement. Given this interface width, we need to ensure there are a sufficient
number of grid points (for finite difference schemes) or mesh elements (for
finite element or finite volume schemes) through the diffuse interface to
adequately resolve the variation of the composition order parameter.
In [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux),
a square domain with dimensions $200 \times 200$ and no-flux boundary
conditions is considered. An example of a mesh convergence study for this
problem using the MOOSE framework phase-field module (a finite element code) is
described. The $200 \times 200$ domain is discretized using increasing numbers
of elements $N_x$ in the $x$ direction and $N_y$ in the $y$ direction,
maintaining $N_x = N_y$ for square elements (using linear Lagrange shape
functions). The simulations with varying numbers of elements are run until a
significant amount of microstructural evolution has occurred. We need to
increase the number of elements until the microstructure at a fixed time no
longer changes with further increases in the number of elements; at this point
the simulation is converged with respect to the mesh resolution.
The simulation initial conditions and the microstructures at $t = 10,000$ are
shown in the figure below.
The dependence on dimensionality is further illustrated by considering cases
where the initial radius is close to the critical radius: $r_\circ = 0.99 r_c$,
$r_\circ = r_c$ and $r_\circ = 1.01 r_c$. The simulation results of radius
evolution are shown above for 2D (left) and 3D (right). As expected from the
the classical homogeneous nucleation theory, the sub-critical nucleus with
$r_\circ = 0.99 r_c$ shrinks and the super-critical nucleus with $r_\circ =
1.01 r_c$ grows.
Since the nucleus in the phase-field model is a diffuse-interface approximation
of the classical sharp interface nucleus, $r_\circ = r_c$ is fairly close to an
unstable equilibrium. Ideally, the radius would remain constant with
time. However, since the system is unstable, small numerical errors accumulate
with time, eventually leading to growth or shrinkage of the nucleus. During
initial time steps, the interface profile is expected to undergo some changes
from the starting profile due to equilibration. While the $tanh$ function is a
common choice for the initial condition of the interface, it is an exact
solution only for a planar interface, representative of a 1D scenario.
## Initial conditions
For simulations of the evolution of two or more phases, it is important to
anticipate the expected equilibrium state of the system given the initial
conditions. To do this, one needs the phase diagram as determined by the bulk
contribution of the free energy density.
For example, in simulating phase separation following spinodal decomposition,
it is common to define the initial state of the order parameter as a spatially
uniform field with an added small 'noisy' perturbation with small
amplitude. However, this order parameter must be within the spinodal region of
the phase diagram, i.e., the region where spontaneous decomposition leads to a
decrease in the free energy. Below we show two instances that demonstrate that
choosing different values for the baseline order parameter, $c_{0,\mathrm{base}}$, and
the same initial perturbation term, $\xi(\vec{r})$, for the initial conditions
of leads to different dynamics.


## Boundary conditions
Boundary conditions (BC) are required to solve for the governing equations in
all phase field simulations. In general, every field must have a defined BC at
every boundary of the system. The three most common types of boundary
conditions (BC) for phase field simulation are:
- Dirichlet BC: The value of a field is specified at the boundary. This type of
boundary condition is useful whenever we want to impose a value to an order
parameter or field at one or more boundaries. Some common examples include
setting a constant value for temperature to simulate a heat reservoir, or
setting a constant value for a solid/liquid order parameter to indicate a
fixed phase beyond the confines of the system.
- Neumann BC: The value of the spatial derivative of a field is specified at
the boundary. This type of boundary conditions is useful to specify fluxes of
fields at the boundary. For example, setting natural BC (a special case of
Neumann BC) for a field at the boundary enforces that the normal component of
gradient of that field is zero along that boundary. Therefore, if a flux for
that field is proportional to this gradient, natural BC is equivalent to
imposing zero flux at the boundary. This BC is convenient to ensure that the
field is conserved. In addition, natural BCs are useful to exploit known
symmetries in the morphology of domains: for example a spherical domain can
be simulated using a quarter (in 2D) or eighth of a system (in 3D) by placing
centering the sphere in a corner of the system and imposing natural BCs along
the boundaries that define the corner.
- Periodic BCs: The value of the field in a boundary with periodic BC matches
the value from the opposite boundary. These type of BCs are useful to
simulate periodic domains, but also to minimize boundary effects. since the
system does not interact with borders.
### Try different boundary conditions and check their impact
We used the results from Benchmark [Problem 1a](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(a)-Square-periodic)
and [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
to analyze the effect of boundary conditions. In addition, we solved for
Cahn-Hilliard dynamics under the same initial condition and simulation
parameters as problem 1 but using mixed boundary conditions, i.e., different
boundary conditions for each boundary. We compare the results for each case at
simulation time _t_ = 1000. The simulations were carried out in the PRISMS-PF
framework using a uniform square mesh with $N_x = N_y = 128$ linear elements
and a time step, $\Delta t$ = 0.005. The results are shown in the figure below.

As can be seen in the figure above, for periodic boundary boundaries the
$\alpha$ - $\beta$ domains are **continuous** on opposite sides of the
system. For no-flux boundaries, the $\alpha$ - $\beta$ interfaces are
**normal** to the boundary. For Dirichlet boundaries (bottom boundary of the
right panel), the value of _c_ is **fixed** along the boundary.
## Interface width
Phase-field modeling is a diffuse interface approach, meaning that interfaces
are represented by a smooth variation of one or more order parameters across
the interface. The width of the interface is a function of the model parameters
and the interface width is determined by model parameter choices. In some
cases, an analytical expression is available that relates interface width to
phase-field model parameters (such as free energy barrier height and gradient
energy coefficient, which also impact the interfacial energy). In other cases,
no analytical solution is available and the interface width must be
approximated or determined numerically based on parameter choices. Such details
are specific to the formulation being used.
Once the relationship between model parameters and interface width is
understood, an appropriate selection of interface width needs to be made (while
maintaining the correct interfacial energy for the system being studied). In
some cases, the interface width in the phase-field model can be chosen to match
the actual physical width of the interface being studied (such typically
sub-nanometer). However, resolving a physically realistic interface width
requires a sub-nanometer grid/mesh (grid/mesh convergence is described further
in the next section). Using a physically realistic interface width often makes
it computationally unfeasible to simulate systems large enough to be
statistically representative. Therefore, in many cases an interfacial width
that is much larger than the the physical width of an interface is used. In
these cases, a careful balance between computational efficiency and model
accuracy is needed; the interface width should be chosen to be small enough
that the physics of the system are accurately represented, while maintaining
adequate computational performance. A useful rule of thumb as a starting point
is that the interface width should be at least an order of magnitude smaller
than the smallest microstructural feature size of interest. Starting from this
guideline, simulations of microstructural evolution with varying interface
widths can be run to ensure that the choice of interface width does not affect
the simulation results. A small test problem may be useful for testing
convergence with respect to interface width; for example a shrinking circular
grain embedded in another grain may be used for testing convergence of a grain
growth model with respect to interface width, rather starting with large,
costly simulations of hundreds of grains.
## Convergence studies
### Carry out grid/mesh convergence study AFTER you have finalized your interfacial width.
As an example of a mesh convergence study, we can consider [Benchmark Problem
1](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/) from the
Phase-Field Community Hub. In this problem, which models spinodal decomposition
using the Cahn-Hilliard equation, the width of the diffuse interface is 4.47,
as defined by the Cahn-Hilliard equation and physical parameters in the problem
statement. Given this interface width, we need to ensure there are a sufficient
number of grid points (for finite difference schemes) or mesh elements (for
finite element or finite volume schemes) through the diffuse interface to
adequately resolve the variation of the composition order parameter.
In [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux),
a square domain with dimensions $200 \times 200$ and no-flux boundary
conditions is considered. An example of a mesh convergence study for this
problem using the MOOSE framework phase-field module (a finite element code) is
described. The $200 \times 200$ domain is discretized using increasing numbers
of elements $N_x$ in the $x$ direction and $N_y$ in the $y$ direction,
maintaining $N_x = N_y$ for square elements (using linear Lagrange shape
functions). The simulations with varying numbers of elements are run until a
significant amount of microstructural evolution has occurred. We need to
increase the number of elements until the microstructure at a fixed time no
longer changes with further increases in the number of elements; at this point
the simulation is converged with respect to the mesh resolution.
The simulation initial conditions and the microstructures at $t = 10,000$ are
shown in the figure below.
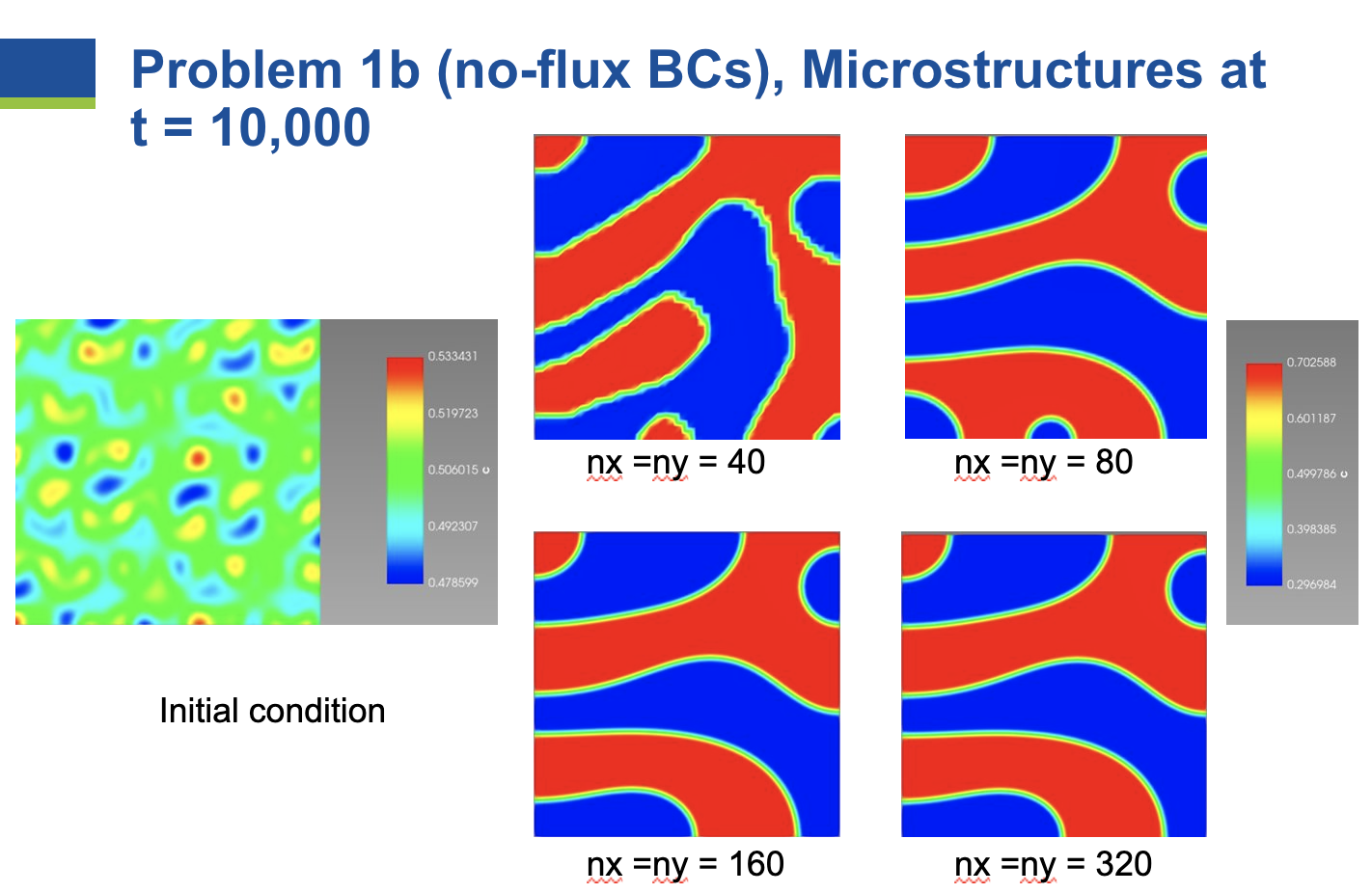 As the number of elements in each direction is increased from 40 to 80 to 160,
changes in the microstructure are observed. However, once the number of
elements increases to 320, no further changes are observed in the
microstructure. Therefore, the problem is converged with respect to mesh
resolution at $N_x = N_y = 160$. For this number of elements, each element has
size $\Delta x = \Delta y$ = 200 / 160 = 1.25. Therefore, the number of
elements through the diffuse interface width is 4.47 / 1.25 = 3.6. Practical
experience in the phase-field community has shown that somewhere between 3 to 5
elements through the interface are usually required to obtain mesh convergence;
however, the appropriate resolution is problem-specific, and convergence should
be tested for the specific physics and parameters at hand.
### Carry out time step convergence studies. Try higher-order schemes, adaptive time stepping, etc. For explicit time integration, know your stability limit.
For codes that use explicit time integration, there is a maximum value of the
time step beyond which the solution becomes numerically unstable. This
stability limit can be determined by the Courant–Friedrichs–Lewy (CFL)
condition and, in general, it strongly depends on the order of the spatial
derivatives. Below we show the simulation results of [Benchmark Problem
1b](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
using time step values slightly below and slightly above the stability
limit. We employed a forward Euler time-integration scheme and spatially
discretized the system using $128 \times 128$ first order elements. The
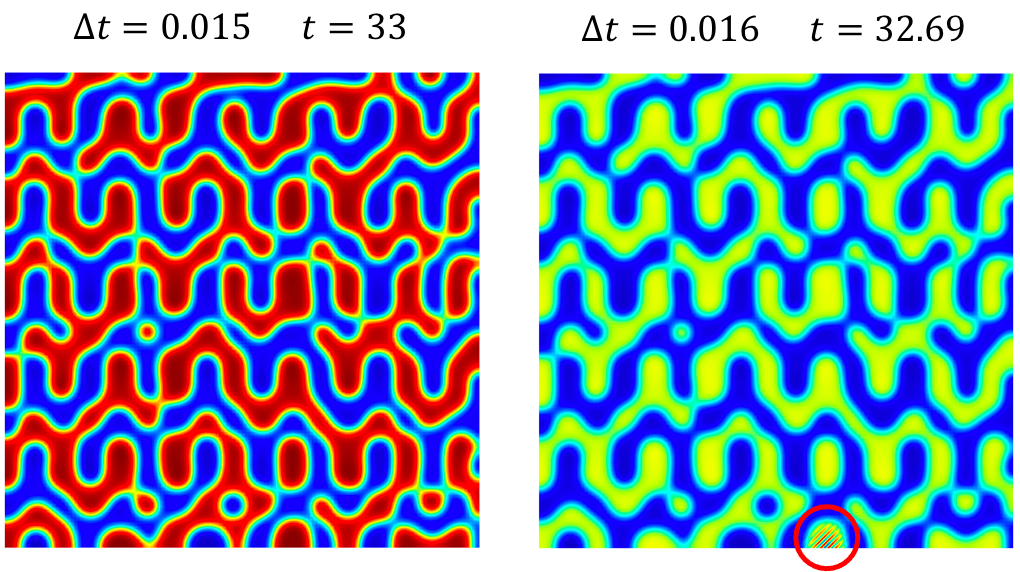
simulations were performed in the PRISMS-PF framework. The left panel of the
figure below shows a snapshot of the concentration at time $t=33$, which was
obtained using a stable time step of $\Delta t=0.015$. If the time step is
increased to $\Delta t=0.016$, the time step goes above the stability
limit. The right panel shows the concentration at time $t \simeq 32.39$ for
$\Delta t=0.016$ and features a numerical instability that appears near the
bottom boundary. After only four time steps the amplification of this
instability caused the simulation to fail.
As the number of elements in each direction is increased from 40 to 80 to 160,
changes in the microstructure are observed. However, once the number of
elements increases to 320, no further changes are observed in the
microstructure. Therefore, the problem is converged with respect to mesh
resolution at $N_x = N_y = 160$. For this number of elements, each element has
size $\Delta x = \Delta y$ = 200 / 160 = 1.25. Therefore, the number of
elements through the diffuse interface width is 4.47 / 1.25 = 3.6. Practical
experience in the phase-field community has shown that somewhere between 3 to 5
elements through the interface are usually required to obtain mesh convergence;
however, the appropriate resolution is problem-specific, and convergence should
be tested for the specific physics and parameters at hand.
### Carry out time step convergence studies. Try higher-order schemes, adaptive time stepping, etc. For explicit time integration, know your stability limit.
For codes that use explicit time integration, there is a maximum value of the
time step beyond which the solution becomes numerically unstable. This
stability limit can be determined by the Courant–Friedrichs–Lewy (CFL)
condition and, in general, it strongly depends on the order of the spatial
derivatives. Below we show the simulation results of [Benchmark Problem
1b](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
using time step values slightly below and slightly above the stability
limit. We employed a forward Euler time-integration scheme and spatially
discretized the system using $128 \times 128$ first order elements. The
simulations were performed in the PRISMS-PF framework. The left panel of the
figure below shows a snapshot of the concentration at time $t=33$, which was
obtained using a stable time step of $\Delta t=0.015$. If the time step is
increased to $\Delta t=0.016$, the time step goes above the stability
limit. The right panel shows the concentration at time $t \simeq 32.39$ for
$\Delta t=0.016$ and features a numerical instability that appears near the
bottom boundary. After only four time steps the amplification of this
instability caused the simulation to fail.
 Codes that use implicit time stepping schemes may have fewer restrictions with
respect to stability as time step size is increased, depending on the
problem. However, discretization error still occurs in implicit schemes and
increases with the size of the time step taken. Therefore, a convergence study
should be carried out to ensure that the size of the time step does not affect
the simulation results. As an example, we can again consider [Benchmark Problem
1](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/) from the
Phase-Field Community Hub. [Problem
1b](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
was solved with the phase-field module from the MOOSE framework using $N_x =
N_y = 160$. The results are shown below. The microstructure at $t = 1000$
remains the same for $\Delta t = 0.1$, $\Delta t = 0.25$, and $\Delta t =
0.5$. Some differences in the microstructure are observed at $\Delta t = 1$,
and further differences become apparent at $\Delta t = 4$. In practice, it is
recommended to start with a given time step and gradually decrease it until no
changes are apparent with further decreases in time step size.

Adaptive time stepping can be useful to increase the time step size during time
periods in the simulation where there are fewer microstructural changes,
particularly for codes that use implicit time stepping schemes. However,
convergence must still be checked for the parameters of the time stepping
scheme being used. An example is the IterationAdaptiveDt time stepping scheme
used in the MOOSE framework. This scheme attempts to increase or decrease the
time step to keep the solver using a certain number of nonlinear iterations
(controlled by the parameter `optimal_iterations`), within a window or plus or
minus the parameter `iteration_window`. Higher values of `optimal_iterations`
parameter result in higher time steps, and with that comes the risk of
discretization error changing simulation results. As shown in the following,
for [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux),
`optimal_iterations` values of 6 or 8 gave results consistent with the
converged time step of 0.5, but when `optimal_iterations` was significantly
increased to 15, changes in the microstructure resulted.

## Impact of Orientation
Oftentimes, the results of the phase field simulations are sensitive to the
orientation and alignment of the key microstructural features with the
mesh/grid points. To demonstrate this we pick a simple solidification problem
with dendritic structure formation. In this case, we utilize the solidification
[example](https://github.com/idaholab/moose/blob/next/modules/phase_field/examples/anisotropic_interfaces/snow.i)
from the MOOSE-based phase field module. This example problem can quickly
demonstrate dendritic structure formation including the formation of secondary
dendritic arms in a computationally cost-effective manner. Here, we use 4-fold
symmetry of the structure and vary the reference angles to misorient the
dendritic arms with respect to the mesh. Dendritic structures corresponding to
0 and 45 degree reference angle is presented below:
Codes that use implicit time stepping schemes may have fewer restrictions with
respect to stability as time step size is increased, depending on the
problem. However, discretization error still occurs in implicit schemes and
increases with the size of the time step taken. Therefore, a convergence study
should be carried out to ensure that the size of the time step does not affect
the simulation results. As an example, we can again consider [Benchmark Problem
1](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/) from the
Phase-Field Community Hub. [Problem
1b](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
was solved with the phase-field module from the MOOSE framework using $N_x =
N_y = 160$. The results are shown below. The microstructure at $t = 1000$
remains the same for $\Delta t = 0.1$, $\Delta t = 0.25$, and $\Delta t =
0.5$. Some differences in the microstructure are observed at $\Delta t = 1$,
and further differences become apparent at $\Delta t = 4$. In practice, it is
recommended to start with a given time step and gradually decrease it until no
changes are apparent with further decreases in time step size.

Adaptive time stepping can be useful to increase the time step size during time
periods in the simulation where there are fewer microstructural changes,
particularly for codes that use implicit time stepping schemes. However,
convergence must still be checked for the parameters of the time stepping
scheme being used. An example is the IterationAdaptiveDt time stepping scheme
used in the MOOSE framework. This scheme attempts to increase or decrease the
time step to keep the solver using a certain number of nonlinear iterations
(controlled by the parameter `optimal_iterations`), within a window or plus or
minus the parameter `iteration_window`. Higher values of `optimal_iterations`
parameter result in higher time steps, and with that comes the risk of
discretization error changing simulation results. As shown in the following,
for [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux),
`optimal_iterations` values of 6 or 8 gave results consistent with the
converged time step of 0.5, but when `optimal_iterations` was significantly
increased to 15, changes in the microstructure resulted.

## Impact of Orientation
Oftentimes, the results of the phase field simulations are sensitive to the
orientation and alignment of the key microstructural features with the
mesh/grid points. To demonstrate this we pick a simple solidification problem
with dendritic structure formation. In this case, we utilize the solidification
[example](https://github.com/idaholab/moose/blob/next/modules/phase_field/examples/anisotropic_interfaces/snow.i)
from the MOOSE-based phase field module. This example problem can quickly
demonstrate dendritic structure formation including the formation of secondary
dendritic arms in a computationally cost-effective manner. Here, we use 4-fold
symmetry of the structure and vary the reference angles to misorient the
dendritic arms with respect to the mesh. Dendritic structures corresponding to
0 and 45 degree reference angle is presented below:

 It is noteworthy that the shape of the dendrite varies with orientation (as
observed by the difference in the dendrite center). For better comparison, we
rotate the $45^{\circ}$ dendrite to align the primary dendrite arms with the
reference orientation dendrite:
It is noteworthy that the shape of the dendrite varies with orientation (as
observed by the difference in the dendrite center). For better comparison, we
rotate the $45^{\circ}$ dendrite to align the primary dendrite arms with the
reference orientation dendrite:
 This highlights the slight differences between the dendrite shapes, especially
the center and the secondary dendritic arms. Additionally, the growth rate of
the solid also varies with orientation as observed by the change in solid area
fraction over time:
This highlights the slight differences between the dendrite shapes, especially
the center and the secondary dendritic arms. Additionally, the growth rate of
the solid also varies with orientation as observed by the change in solid area
fraction over time:
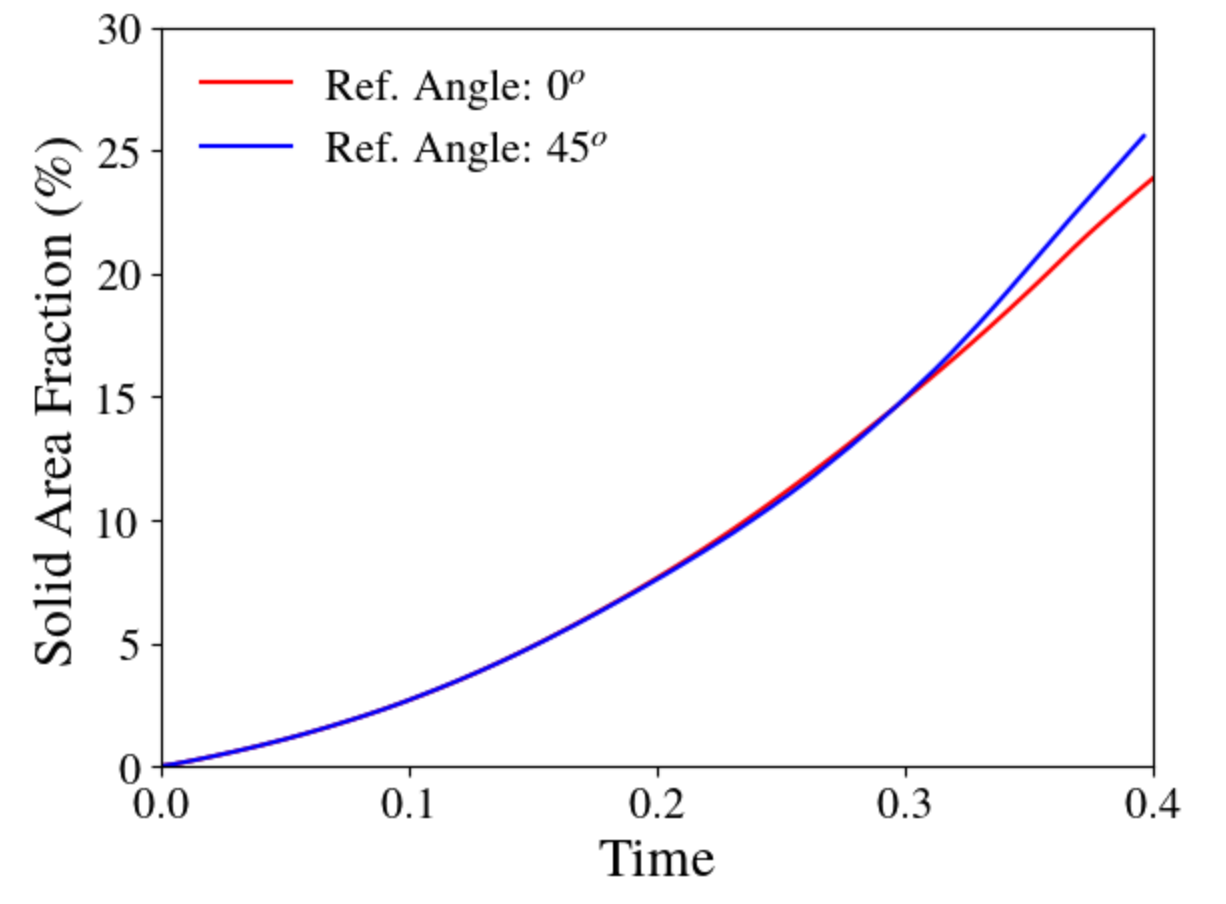 Thus, it is important to evaluate the effect of orientation on the results by
misaligning the grids. Furthermore, these effects are influenced by the
discretization of the mesh. Hence, it is important to ensure that the mesh is
refined enough to properly resolve the interfaces (if necessary, run a mesh
convergence study). For more information about strategies to simulate multiple
dendrites with varying orientation, please refer to examples by Biswas et
al. [[1]](#1), Warren et al. [[2]](#2), Dorr et al. [[3]](#3), Ofori-Opoku et
al. [[4]](#4), and Pusztai et al. [[5]](#5), among others.
## Kinetics and how long to run
The amount of time the simulation should be run depends on the science or
engineering question to be answered, and on the system being studied. For many
classic phase-field problems such as grain growth and coarsening, a
characteristic feature size of the system increases with time, and the progress
of microstructural evolution slows as the characteristic feature size
increases. For example, in grain growth, at long times the mean grain diameter
$D$ increases with time as $D \propto t^{1/2}$. Another example is coarsening
of spherical particles in a matrix; for sufficiently low volume fraction of
particles in a matrix where solute is transported by diffusion, the mean
particle radius $R$ increases with time as $R \propto t^{1/3}$.
It is also useful to be aware that the system may reach a metastable or stable
equilibrium state with respect to system energy, in which case no further
microstructural evolution will occur for increasing simulation time. In the
grain growth example, if the system evolves to a single grain, stable
equilbrium has been reached. If the system evolves to a two-grain configuration
with a flat grain boundary between the grains, it has reached a metastable
equilibrium; the system could still lower it energy by removing the grain
boundary, but in that configuration, there is no kinetic driving force to
remove it from the metastable state. To monitor for such possibilities, it is
useful for the simulation to periodically output the total free energy of the
system; a stable or metastable equilibrium state is indicated by a constant
free energy with respect to time.
## References
[1]
Biswas et al., “Solidification and grain formation in alloys: a 2D application
of the grand-potential-based phase-field approach”, Modelling and Simulation in
Materials Science and Engineering, 30 (2022) 025013. DOI:
[10.1088/1361-651X/ac46dc](https://doi.org/10.1088/1361-651X/ac46dc).
[2]
Warren et al., “Extending phase field models of solidification to
polycrystalline materials”, Acta Materialia 51 (2003) 6035–6058. DOI:
[10.1016/S1359-6454(03)00388-4](https://doi.org/10.1016/S1359-6454(03)00388-4).
[3]
Dorr et al., “A numerical algorithm for the solution of a phase-field model of
polycrystalline materials”, Journal of Computational Physics 229 (2010)
626–641. DOI:
[10.1016/j.jcp.2009.09.041](https://doi.org/10.1016/j.jcp.2009.09.041).
[4]
Ofori-Opuku et al., “A quantitative multi-phase field model of polycrystalline
alloy solidification”, Acta Materialia 58 (2010) 2155-2164. DOI:
[10.1016/j.actamat.2009.12.001](https://doi.org/10.1016/j.actamat.2009.12.001)
[5]
Pusztai et al., “Phase-field approach to polycrystalline solidification
including heterogeneous and homogeneous nucleation”, Journal of Physics:
Condensed Matter 20 (2008) 404205. DOI:
[10.1088/0953-8984/20/40/404205](https://doi.org/10.1088/0953-8984/20/40/404205).
Thus, it is important to evaluate the effect of orientation on the results by
misaligning the grids. Furthermore, these effects are influenced by the
discretization of the mesh. Hence, it is important to ensure that the mesh is
refined enough to properly resolve the interfaces (if necessary, run a mesh
convergence study). For more information about strategies to simulate multiple
dendrites with varying orientation, please refer to examples by Biswas et
al. [[1]](#1), Warren et al. [[2]](#2), Dorr et al. [[3]](#3), Ofori-Opoku et
al. [[4]](#4), and Pusztai et al. [[5]](#5), among others.
## Kinetics and how long to run
The amount of time the simulation should be run depends on the science or
engineering question to be answered, and on the system being studied. For many
classic phase-field problems such as grain growth and coarsening, a
characteristic feature size of the system increases with time, and the progress
of microstructural evolution slows as the characteristic feature size
increases. For example, in grain growth, at long times the mean grain diameter
$D$ increases with time as $D \propto t^{1/2}$. Another example is coarsening
of spherical particles in a matrix; for sufficiently low volume fraction of
particles in a matrix where solute is transported by diffusion, the mean
particle radius $R$ increases with time as $R \propto t^{1/3}$.
It is also useful to be aware that the system may reach a metastable or stable
equilibrium state with respect to system energy, in which case no further
microstructural evolution will occur for increasing simulation time. In the
grain growth example, if the system evolves to a single grain, stable
equilbrium has been reached. If the system evolves to a two-grain configuration
with a flat grain boundary between the grains, it has reached a metastable
equilibrium; the system could still lower it energy by removing the grain
boundary, but in that configuration, there is no kinetic driving force to
remove it from the metastable state. To monitor for such possibilities, it is
useful for the simulation to periodically output the total free energy of the
system; a stable or metastable equilibrium state is indicated by a constant
free energy with respect to time.
## References
[1]
Biswas et al., “Solidification and grain formation in alloys: a 2D application
of the grand-potential-based phase-field approach”, Modelling and Simulation in
Materials Science and Engineering, 30 (2022) 025013. DOI:
[10.1088/1361-651X/ac46dc](https://doi.org/10.1088/1361-651X/ac46dc).
[2]
Warren et al., “Extending phase field models of solidification to
polycrystalline materials”, Acta Materialia 51 (2003) 6035–6058. DOI:
[10.1016/S1359-6454(03)00388-4](https://doi.org/10.1016/S1359-6454(03)00388-4).
[3]
Dorr et al., “A numerical algorithm for the solution of a phase-field model of
polycrystalline materials”, Journal of Computational Physics 229 (2010)
626–641. DOI:
[10.1016/j.jcp.2009.09.041](https://doi.org/10.1016/j.jcp.2009.09.041).
[4]
Ofori-Opuku et al., “A quantitative multi-phase field model of polycrystalline
alloy solidification”, Acta Materialia 58 (2010) 2155-2164. DOI:
[10.1016/j.actamat.2009.12.001](https://doi.org/10.1016/j.actamat.2009.12.001)
[5]
Pusztai et al., “Phase-field approach to polycrystalline solidification
including heterogeneous and homogeneous nucleation”, Journal of Physics:
Condensed Matter 20 (2008) 404205. DOI:
[10.1088/0953-8984/20/40/404205](https://doi.org/10.1088/0953-8984/20/40/404205).

 The time evolution of the order parameter, given by the Allen-Cahn equation,
was solved using the MOOSE framework. Details of the numerical method can be
found in [Wu _et al._ (2021)](
https://www.sciencedirect.com/science/article/abs/pii/S0927025621000963?via%3Dihub).
The simulations results of nucleus evolution are shown in the figures below:
(left) order parameter profile measured radially from the center of domain at
different evolution times; (right) radius as a function of evolution time. We
see that the seed of same starting radius $r_\circ = 7.5$ units evolves starkly
differently in 2D and 3D. While the nucleus grows in 2D, it shrinks and
dissolves in 3D.
The time evolution of the order parameter, given by the Allen-Cahn equation,
was solved using the MOOSE framework. Details of the numerical method can be
found in [Wu _et al._ (2021)](
https://www.sciencedirect.com/science/article/abs/pii/S0927025621000963?via%3Dihub).
The simulations results of nucleus evolution are shown in the figures below:
(left) order parameter profile measured radially from the center of domain at
different evolution times; (right) radius as a function of evolution time. We
see that the seed of same starting radius $r_\circ = 7.5$ units evolves starkly
differently in 2D and 3D. While the nucleus grows in 2D, it shrinks and
dissolves in 3D.



 The dependence on dimensionality is further illustrated by considering cases
where the initial radius is close to the critical radius: $r_\circ = 0.99 r_c$,
$r_\circ = r_c$ and $r_\circ = 1.01 r_c$. The simulation results of radius
evolution are shown above for 2D (left) and 3D (right). As expected from the
the classical homogeneous nucleation theory, the sub-critical nucleus with
$r_\circ = 0.99 r_c$ shrinks and the super-critical nucleus with $r_\circ =
1.01 r_c$ grows.
Since the nucleus in the phase-field model is a diffuse-interface approximation
of the classical sharp interface nucleus, $r_\circ = r_c$ is fairly close to an
unstable equilibrium. Ideally, the radius would remain constant with
time. However, since the system is unstable, small numerical errors accumulate
with time, eventually leading to growth or shrinkage of the nucleus. During
initial time steps, the interface profile is expected to undergo some changes
from the starting profile due to equilibration. While the $tanh$ function is a
common choice for the initial condition of the interface, it is an exact
solution only for a planar interface, representative of a 1D scenario.
## Initial conditions
For simulations of the evolution of two or more phases, it is important to
anticipate the expected equilibrium state of the system given the initial
conditions. To do this, one needs the phase diagram as determined by the bulk
contribution of the free energy density.
For example, in simulating phase separation following spinodal decomposition,
it is common to define the initial state of the order parameter as a spatially
uniform field with an added small 'noisy' perturbation with small
amplitude. However, this order parameter must be within the spinodal region of
the phase diagram, i.e., the region where spontaneous decomposition leads to a
decrease in the free energy. Below we show two instances that demonstrate that
choosing different values for the baseline order parameter, $c_{0,\mathrm{base}}$, and
the same initial perturbation term, $\xi(\vec{r})$, for the initial conditions
of leads to different dynamics.


## Boundary conditions
Boundary conditions (BC) are required to solve for the governing equations in
all phase field simulations. In general, every field must have a defined BC at
every boundary of the system. The three most common types of boundary
conditions (BC) for phase field simulation are:
- Dirichlet BC: The value of a field is specified at the boundary. This type of
boundary condition is useful whenever we want to impose a value to an order
parameter or field at one or more boundaries. Some common examples include
setting a constant value for temperature to simulate a heat reservoir, or
setting a constant value for a solid/liquid order parameter to indicate a
fixed phase beyond the confines of the system.
- Neumann BC: The value of the spatial derivative of a field is specified at
the boundary. This type of boundary conditions is useful to specify fluxes of
fields at the boundary. For example, setting natural BC (a special case of
Neumann BC) for a field at the boundary enforces that the normal component of
gradient of that field is zero along that boundary. Therefore, if a flux for
that field is proportional to this gradient, natural BC is equivalent to
imposing zero flux at the boundary. This BC is convenient to ensure that the
field is conserved. In addition, natural BCs are useful to exploit known
symmetries in the morphology of domains: for example a spherical domain can
be simulated using a quarter (in 2D) or eighth of a system (in 3D) by placing
centering the sphere in a corner of the system and imposing natural BCs along
the boundaries that define the corner.
- Periodic BCs: The value of the field in a boundary with periodic BC matches
the value from the opposite boundary. These type of BCs are useful to
simulate periodic domains, but also to minimize boundary effects. since the
system does not interact with borders.
### Try different boundary conditions and check their impact
We used the results from Benchmark [Problem 1a](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(a)-Square-periodic)
and [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
to analyze the effect of boundary conditions. In addition, we solved for
Cahn-Hilliard dynamics under the same initial condition and simulation
parameters as problem 1 but using mixed boundary conditions, i.e., different
boundary conditions for each boundary. We compare the results for each case at
simulation time _t_ = 1000. The simulations were carried out in the PRISMS-PF
framework using a uniform square mesh with $N_x = N_y = 128$ linear elements
and a time step, $\Delta t$ = 0.005. The results are shown in the figure below.

As can be seen in the figure above, for periodic boundary boundaries the
$\alpha$ - $\beta$ domains are **continuous** on opposite sides of the
system. For no-flux boundaries, the $\alpha$ - $\beta$ interfaces are
**normal** to the boundary. For Dirichlet boundaries (bottom boundary of the
right panel), the value of _c_ is **fixed** along the boundary.
## Interface width
Phase-field modeling is a diffuse interface approach, meaning that interfaces
are represented by a smooth variation of one or more order parameters across
the interface. The width of the interface is a function of the model parameters
and the interface width is determined by model parameter choices. In some
cases, an analytical expression is available that relates interface width to
phase-field model parameters (such as free energy barrier height and gradient
energy coefficient, which also impact the interfacial energy). In other cases,
no analytical solution is available and the interface width must be
approximated or determined numerically based on parameter choices. Such details
are specific to the formulation being used.
Once the relationship between model parameters and interface width is
understood, an appropriate selection of interface width needs to be made (while
maintaining the correct interfacial energy for the system being studied). In
some cases, the interface width in the phase-field model can be chosen to match
the actual physical width of the interface being studied (such typically
sub-nanometer). However, resolving a physically realistic interface width
requires a sub-nanometer grid/mesh (grid/mesh convergence is described further
in the next section). Using a physically realistic interface width often makes
it computationally unfeasible to simulate systems large enough to be
statistically representative. Therefore, in many cases an interfacial width
that is much larger than the the physical width of an interface is used. In
these cases, a careful balance between computational efficiency and model
accuracy is needed; the interface width should be chosen to be small enough
that the physics of the system are accurately represented, while maintaining
adequate computational performance. A useful rule of thumb as a starting point
is that the interface width should be at least an order of magnitude smaller
than the smallest microstructural feature size of interest. Starting from this
guideline, simulations of microstructural evolution with varying interface
widths can be run to ensure that the choice of interface width does not affect
the simulation results. A small test problem may be useful for testing
convergence with respect to interface width; for example a shrinking circular
grain embedded in another grain may be used for testing convergence of a grain
growth model with respect to interface width, rather starting with large,
costly simulations of hundreds of grains.
## Convergence studies
### Carry out grid/mesh convergence study AFTER you have finalized your interfacial width.
As an example of a mesh convergence study, we can consider [Benchmark Problem
1](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/) from the
Phase-Field Community Hub. In this problem, which models spinodal decomposition
using the Cahn-Hilliard equation, the width of the diffuse interface is 4.47,
as defined by the Cahn-Hilliard equation and physical parameters in the problem
statement. Given this interface width, we need to ensure there are a sufficient
number of grid points (for finite difference schemes) or mesh elements (for
finite element or finite volume schemes) through the diffuse interface to
adequately resolve the variation of the composition order parameter.
In [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux),
a square domain with dimensions $200 \times 200$ and no-flux boundary
conditions is considered. An example of a mesh convergence study for this
problem using the MOOSE framework phase-field module (a finite element code) is
described. The $200 \times 200$ domain is discretized using increasing numbers
of elements $N_x$ in the $x$ direction and $N_y$ in the $y$ direction,
maintaining $N_x = N_y$ for square elements (using linear Lagrange shape
functions). The simulations with varying numbers of elements are run until a
significant amount of microstructural evolution has occurred. We need to
increase the number of elements until the microstructure at a fixed time no
longer changes with further increases in the number of elements; at this point
the simulation is converged with respect to the mesh resolution.
The simulation initial conditions and the microstructures at $t = 10,000$ are
shown in the figure below.
The dependence on dimensionality is further illustrated by considering cases
where the initial radius is close to the critical radius: $r_\circ = 0.99 r_c$,
$r_\circ = r_c$ and $r_\circ = 1.01 r_c$. The simulation results of radius
evolution are shown above for 2D (left) and 3D (right). As expected from the
the classical homogeneous nucleation theory, the sub-critical nucleus with
$r_\circ = 0.99 r_c$ shrinks and the super-critical nucleus with $r_\circ =
1.01 r_c$ grows.
Since the nucleus in the phase-field model is a diffuse-interface approximation
of the classical sharp interface nucleus, $r_\circ = r_c$ is fairly close to an
unstable equilibrium. Ideally, the radius would remain constant with
time. However, since the system is unstable, small numerical errors accumulate
with time, eventually leading to growth or shrinkage of the nucleus. During
initial time steps, the interface profile is expected to undergo some changes
from the starting profile due to equilibration. While the $tanh$ function is a
common choice for the initial condition of the interface, it is an exact
solution only for a planar interface, representative of a 1D scenario.
## Initial conditions
For simulations of the evolution of two or more phases, it is important to
anticipate the expected equilibrium state of the system given the initial
conditions. To do this, one needs the phase diagram as determined by the bulk
contribution of the free energy density.
For example, in simulating phase separation following spinodal decomposition,
it is common to define the initial state of the order parameter as a spatially
uniform field with an added small 'noisy' perturbation with small
amplitude. However, this order parameter must be within the spinodal region of
the phase diagram, i.e., the region where spontaneous decomposition leads to a
decrease in the free energy. Below we show two instances that demonstrate that
choosing different values for the baseline order parameter, $c_{0,\mathrm{base}}$, and
the same initial perturbation term, $\xi(\vec{r})$, for the initial conditions
of leads to different dynamics.


## Boundary conditions
Boundary conditions (BC) are required to solve for the governing equations in
all phase field simulations. In general, every field must have a defined BC at
every boundary of the system. The three most common types of boundary
conditions (BC) for phase field simulation are:
- Dirichlet BC: The value of a field is specified at the boundary. This type of
boundary condition is useful whenever we want to impose a value to an order
parameter or field at one or more boundaries. Some common examples include
setting a constant value for temperature to simulate a heat reservoir, or
setting a constant value for a solid/liquid order parameter to indicate a
fixed phase beyond the confines of the system.
- Neumann BC: The value of the spatial derivative of a field is specified at
the boundary. This type of boundary conditions is useful to specify fluxes of
fields at the boundary. For example, setting natural BC (a special case of
Neumann BC) for a field at the boundary enforces that the normal component of
gradient of that field is zero along that boundary. Therefore, if a flux for
that field is proportional to this gradient, natural BC is equivalent to
imposing zero flux at the boundary. This BC is convenient to ensure that the
field is conserved. In addition, natural BCs are useful to exploit known
symmetries in the morphology of domains: for example a spherical domain can
be simulated using a quarter (in 2D) or eighth of a system (in 3D) by placing
centering the sphere in a corner of the system and imposing natural BCs along
the boundaries that define the corner.
- Periodic BCs: The value of the field in a boundary with periodic BC matches
the value from the opposite boundary. These type of BCs are useful to
simulate periodic domains, but also to minimize boundary effects. since the
system does not interact with borders.
### Try different boundary conditions and check their impact
We used the results from Benchmark [Problem 1a](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(a)-Square-periodic)
and [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
to analyze the effect of boundary conditions. In addition, we solved for
Cahn-Hilliard dynamics under the same initial condition and simulation
parameters as problem 1 but using mixed boundary conditions, i.e., different
boundary conditions for each boundary. We compare the results for each case at
simulation time _t_ = 1000. The simulations were carried out in the PRISMS-PF
framework using a uniform square mesh with $N_x = N_y = 128$ linear elements
and a time step, $\Delta t$ = 0.005. The results are shown in the figure below.

As can be seen in the figure above, for periodic boundary boundaries the
$\alpha$ - $\beta$ domains are **continuous** on opposite sides of the
system. For no-flux boundaries, the $\alpha$ - $\beta$ interfaces are
**normal** to the boundary. For Dirichlet boundaries (bottom boundary of the
right panel), the value of _c_ is **fixed** along the boundary.
## Interface width
Phase-field modeling is a diffuse interface approach, meaning that interfaces
are represented by a smooth variation of one or more order parameters across
the interface. The width of the interface is a function of the model parameters
and the interface width is determined by model parameter choices. In some
cases, an analytical expression is available that relates interface width to
phase-field model parameters (such as free energy barrier height and gradient
energy coefficient, which also impact the interfacial energy). In other cases,
no analytical solution is available and the interface width must be
approximated or determined numerically based on parameter choices. Such details
are specific to the formulation being used.
Once the relationship between model parameters and interface width is
understood, an appropriate selection of interface width needs to be made (while
maintaining the correct interfacial energy for the system being studied). In
some cases, the interface width in the phase-field model can be chosen to match
the actual physical width of the interface being studied (such typically
sub-nanometer). However, resolving a physically realistic interface width
requires a sub-nanometer grid/mesh (grid/mesh convergence is described further
in the next section). Using a physically realistic interface width often makes
it computationally unfeasible to simulate systems large enough to be
statistically representative. Therefore, in many cases an interfacial width
that is much larger than the the physical width of an interface is used. In
these cases, a careful balance between computational efficiency and model
accuracy is needed; the interface width should be chosen to be small enough
that the physics of the system are accurately represented, while maintaining
adequate computational performance. A useful rule of thumb as a starting point
is that the interface width should be at least an order of magnitude smaller
than the smallest microstructural feature size of interest. Starting from this
guideline, simulations of microstructural evolution with varying interface
widths can be run to ensure that the choice of interface width does not affect
the simulation results. A small test problem may be useful for testing
convergence with respect to interface width; for example a shrinking circular
grain embedded in another grain may be used for testing convergence of a grain
growth model with respect to interface width, rather starting with large,
costly simulations of hundreds of grains.
## Convergence studies
### Carry out grid/mesh convergence study AFTER you have finalized your interfacial width.
As an example of a mesh convergence study, we can consider [Benchmark Problem
1](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/) from the
Phase-Field Community Hub. In this problem, which models spinodal decomposition
using the Cahn-Hilliard equation, the width of the diffuse interface is 4.47,
as defined by the Cahn-Hilliard equation and physical parameters in the problem
statement. Given this interface width, we need to ensure there are a sufficient
number of grid points (for finite difference schemes) or mesh elements (for
finite element or finite volume schemes) through the diffuse interface to
adequately resolve the variation of the composition order parameter.
In [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux),
a square domain with dimensions $200 \times 200$ and no-flux boundary
conditions is considered. An example of a mesh convergence study for this
problem using the MOOSE framework phase-field module (a finite element code) is
described. The $200 \times 200$ domain is discretized using increasing numbers
of elements $N_x$ in the $x$ direction and $N_y$ in the $y$ direction,
maintaining $N_x = N_y$ for square elements (using linear Lagrange shape
functions). The simulations with varying numbers of elements are run until a
significant amount of microstructural evolution has occurred. We need to
increase the number of elements until the microstructure at a fixed time no
longer changes with further increases in the number of elements; at this point
the simulation is converged with respect to the mesh resolution.
The simulation initial conditions and the microstructures at $t = 10,000$ are
shown in the figure below.
 As the number of elements in each direction is increased from 40 to 80 to 160,
changes in the microstructure are observed. However, once the number of
elements increases to 320, no further changes are observed in the
microstructure. Therefore, the problem is converged with respect to mesh
resolution at $N_x = N_y = 160$. For this number of elements, each element has
size $\Delta x = \Delta y$ = 200 / 160 = 1.25. Therefore, the number of
elements through the diffuse interface width is 4.47 / 1.25 = 3.6. Practical
experience in the phase-field community has shown that somewhere between 3 to 5
elements through the interface are usually required to obtain mesh convergence;
however, the appropriate resolution is problem-specific, and convergence should
be tested for the specific physics and parameters at hand.
### Carry out time step convergence studies. Try higher-order schemes, adaptive time stepping, etc. For explicit time integration, know your stability limit.
For codes that use explicit time integration, there is a maximum value of the
time step beyond which the solution becomes numerically unstable. This
stability limit can be determined by the Courant–Friedrichs–Lewy (CFL)
condition and, in general, it strongly depends on the order of the spatial
derivatives. Below we show the simulation results of [Benchmark Problem
1b](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
using time step values slightly below and slightly above the stability
limit. We employed a forward Euler time-integration scheme and spatially
discretized the system using $128 \times 128$ first order elements. The
simulations were performed in the PRISMS-PF framework. The left panel of the
figure below shows a snapshot of the concentration at time $t=33$, which was
obtained using a stable time step of $\Delta t=0.015$. If the time step is
increased to $\Delta t=0.016$, the time step goes above the stability
limit. The right panel shows the concentration at time $t \simeq 32.39$ for
$\Delta t=0.016$ and features a numerical instability that appears near the
bottom boundary. After only four time steps the amplification of this
instability caused the simulation to fail.
As the number of elements in each direction is increased from 40 to 80 to 160,
changes in the microstructure are observed. However, once the number of
elements increases to 320, no further changes are observed in the
microstructure. Therefore, the problem is converged with respect to mesh
resolution at $N_x = N_y = 160$. For this number of elements, each element has
size $\Delta x = \Delta y$ = 200 / 160 = 1.25. Therefore, the number of
elements through the diffuse interface width is 4.47 / 1.25 = 3.6. Practical
experience in the phase-field community has shown that somewhere between 3 to 5
elements through the interface are usually required to obtain mesh convergence;
however, the appropriate resolution is problem-specific, and convergence should
be tested for the specific physics and parameters at hand.
### Carry out time step convergence studies. Try higher-order schemes, adaptive time stepping, etc. For explicit time integration, know your stability limit.
For codes that use explicit time integration, there is a maximum value of the
time step beyond which the solution becomes numerically unstable. This
stability limit can be determined by the Courant–Friedrichs–Lewy (CFL)
condition and, in general, it strongly depends on the order of the spatial
derivatives. Below we show the simulation results of [Benchmark Problem
1b](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
using time step values slightly below and slightly above the stability
limit. We employed a forward Euler time-integration scheme and spatially
discretized the system using $128 \times 128$ first order elements. The
simulations were performed in the PRISMS-PF framework. The left panel of the
figure below shows a snapshot of the concentration at time $t=33$, which was
obtained using a stable time step of $\Delta t=0.015$. If the time step is
increased to $\Delta t=0.016$, the time step goes above the stability
limit. The right panel shows the concentration at time $t \simeq 32.39$ for
$\Delta t=0.016$ and features a numerical instability that appears near the
bottom boundary. After only four time steps the amplification of this
instability caused the simulation to fail.
 Codes that use implicit time stepping schemes may have fewer restrictions with
respect to stability as time step size is increased, depending on the
problem. However, discretization error still occurs in implicit schemes and
increases with the size of the time step taken. Therefore, a convergence study
should be carried out to ensure that the size of the time step does not affect
the simulation results. As an example, we can again consider [Benchmark Problem
1](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/) from the
Phase-Field Community Hub. [Problem
1b](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
was solved with the phase-field module from the MOOSE framework using $N_x =
N_y = 160$. The results are shown below. The microstructure at $t = 1000$
remains the same for $\Delta t = 0.1$, $\Delta t = 0.25$, and $\Delta t =
0.5$. Some differences in the microstructure are observed at $\Delta t = 1$,
and further differences become apparent at $\Delta t = 4$. In practice, it is
recommended to start with a given time step and gradually decrease it until no
changes are apparent with further decreases in time step size.

Adaptive time stepping can be useful to increase the time step size during time
periods in the simulation where there are fewer microstructural changes,
particularly for codes that use implicit time stepping schemes. However,
convergence must still be checked for the parameters of the time stepping
scheme being used. An example is the IterationAdaptiveDt time stepping scheme
used in the MOOSE framework. This scheme attempts to increase or decrease the
time step to keep the solver using a certain number of nonlinear iterations
(controlled by the parameter `optimal_iterations`), within a window or plus or
minus the parameter `iteration_window`. Higher values of `optimal_iterations`
parameter result in higher time steps, and with that comes the risk of
discretization error changing simulation results. As shown in the following,
for [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux),
`optimal_iterations` values of 6 or 8 gave results consistent with the
converged time step of 0.5, but when `optimal_iterations` was significantly
increased to 15, changes in the microstructure resulted.

## Impact of Orientation
Oftentimes, the results of the phase field simulations are sensitive to the
orientation and alignment of the key microstructural features with the
mesh/grid points. To demonstrate this we pick a simple solidification problem
with dendritic structure formation. In this case, we utilize the solidification
[example](https://github.com/idaholab/moose/blob/next/modules/phase_field/examples/anisotropic_interfaces/snow.i)
from the MOOSE-based phase field module. This example problem can quickly
demonstrate dendritic structure formation including the formation of secondary
dendritic arms in a computationally cost-effective manner. Here, we use 4-fold
symmetry of the structure and vary the reference angles to misorient the
dendritic arms with respect to the mesh. Dendritic structures corresponding to
0 and 45 degree reference angle is presented below:
Codes that use implicit time stepping schemes may have fewer restrictions with
respect to stability as time step size is increased, depending on the
problem. However, discretization error still occurs in implicit schemes and
increases with the size of the time step taken. Therefore, a convergence study
should be carried out to ensure that the size of the time step does not affect
the simulation results. As an example, we can again consider [Benchmark Problem
1](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/) from the
Phase-Field Community Hub. [Problem
1b](https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux)
was solved with the phase-field module from the MOOSE framework using $N_x =
N_y = 160$. The results are shown below. The microstructure at $t = 1000$
remains the same for $\Delta t = 0.1$, $\Delta t = 0.25$, and $\Delta t =
0.5$. Some differences in the microstructure are observed at $\Delta t = 1$,
and further differences become apparent at $\Delta t = 4$. In practice, it is
recommended to start with a given time step and gradually decrease it until no
changes are apparent with further decreases in time step size.

Adaptive time stepping can be useful to increase the time step size during time
periods in the simulation where there are fewer microstructural changes,
particularly for codes that use implicit time stepping schemes. However,
convergence must still be checked for the parameters of the time stepping
scheme being used. An example is the IterationAdaptiveDt time stepping scheme
used in the MOOSE framework. This scheme attempts to increase or decrease the
time step to keep the solver using a certain number of nonlinear iterations
(controlled by the parameter `optimal_iterations`), within a window or plus or
minus the parameter `iteration_window`. Higher values of `optimal_iterations`
parameter result in higher time steps, and with that comes the risk of
discretization error changing simulation results. As shown in the following,
for [Problem 1b](
https://pages.nist.gov/pfhub/benchmarks/benchmark1.ipynb/#(b)-Square-no-flux),
`optimal_iterations` values of 6 or 8 gave results consistent with the
converged time step of 0.5, but when `optimal_iterations` was significantly
increased to 15, changes in the microstructure resulted.

## Impact of Orientation
Oftentimes, the results of the phase field simulations are sensitive to the
orientation and alignment of the key microstructural features with the
mesh/grid points. To demonstrate this we pick a simple solidification problem
with dendritic structure formation. In this case, we utilize the solidification
[example](https://github.com/idaholab/moose/blob/next/modules/phase_field/examples/anisotropic_interfaces/snow.i)
from the MOOSE-based phase field module. This example problem can quickly
demonstrate dendritic structure formation including the formation of secondary
dendritic arms in a computationally cost-effective manner. Here, we use 4-fold
symmetry of the structure and vary the reference angles to misorient the
dendritic arms with respect to the mesh. Dendritic structures corresponding to
0 and 45 degree reference angle is presented below:

 It is noteworthy that the shape of the dendrite varies with orientation (as
observed by the difference in the dendrite center). For better comparison, we
rotate the $45^{\circ}$ dendrite to align the primary dendrite arms with the
reference orientation dendrite:
It is noteworthy that the shape of the dendrite varies with orientation (as
observed by the difference in the dendrite center). For better comparison, we
rotate the $45^{\circ}$ dendrite to align the primary dendrite arms with the
reference orientation dendrite:
 This highlights the slight differences between the dendrite shapes, especially
the center and the secondary dendritic arms. Additionally, the growth rate of
the solid also varies with orientation as observed by the change in solid area
fraction over time:
This highlights the slight differences between the dendrite shapes, especially
the center and the secondary dendritic arms. Additionally, the growth rate of
the solid also varies with orientation as observed by the change in solid area
fraction over time:
 Thus, it is important to evaluate the effect of orientation on the results by
misaligning the grids. Furthermore, these effects are influenced by the
discretization of the mesh. Hence, it is important to ensure that the mesh is
refined enough to properly resolve the interfaces (if necessary, run a mesh
convergence study). For more information about strategies to simulate multiple
dendrites with varying orientation, please refer to examples by Biswas et
al. [[1]](#1), Warren et al. [[2]](#2), Dorr et al. [[3]](#3), Ofori-Opoku et
al. [[4]](#4), and Pusztai et al. [[5]](#5), among others.
## Kinetics and how long to run
The amount of time the simulation should be run depends on the science or
engineering question to be answered, and on the system being studied. For many
classic phase-field problems such as grain growth and coarsening, a
characteristic feature size of the system increases with time, and the progress
of microstructural evolution slows as the characteristic feature size
increases. For example, in grain growth, at long times the mean grain diameter
$D$ increases with time as $D \propto t^{1/2}$. Another example is coarsening
of spherical particles in a matrix; for sufficiently low volume fraction of
particles in a matrix where solute is transported by diffusion, the mean
particle radius $R$ increases with time as $R \propto t^{1/3}$.
It is also useful to be aware that the system may reach a metastable or stable
equilibrium state with respect to system energy, in which case no further
microstructural evolution will occur for increasing simulation time. In the
grain growth example, if the system evolves to a single grain, stable
equilbrium has been reached. If the system evolves to a two-grain configuration
with a flat grain boundary between the grains, it has reached a metastable
equilibrium; the system could still lower it energy by removing the grain
boundary, but in that configuration, there is no kinetic driving force to
remove it from the metastable state. To monitor for such possibilities, it is
useful for the simulation to periodically output the total free energy of the
system; a stable or metastable equilibrium state is indicated by a constant
free energy with respect to time.
## References
[1]
Biswas et al., “Solidification and grain formation in alloys: a 2D application
of the grand-potential-based phase-field approach”, Modelling and Simulation in
Materials Science and Engineering, 30 (2022) 025013. DOI:
[10.1088/1361-651X/ac46dc](https://doi.org/10.1088/1361-651X/ac46dc).
[2]
Warren et al., “Extending phase field models of solidification to
polycrystalline materials”, Acta Materialia 51 (2003) 6035–6058. DOI:
[10.1016/S1359-6454(03)00388-4](https://doi.org/10.1016/S1359-6454(03)00388-4).
[3]
Dorr et al., “A numerical algorithm for the solution of a phase-field model of
polycrystalline materials”, Journal of Computational Physics 229 (2010)
626–641. DOI:
[10.1016/j.jcp.2009.09.041](https://doi.org/10.1016/j.jcp.2009.09.041).
[4]
Ofori-Opuku et al., “A quantitative multi-phase field model of polycrystalline
alloy solidification”, Acta Materialia 58 (2010) 2155-2164. DOI:
[10.1016/j.actamat.2009.12.001](https://doi.org/10.1016/j.actamat.2009.12.001)
[5]
Pusztai et al., “Phase-field approach to polycrystalline solidification
including heterogeneous and homogeneous nucleation”, Journal of Physics:
Condensed Matter 20 (2008) 404205. DOI:
[10.1088/0953-8984/20/40/404205](https://doi.org/10.1088/0953-8984/20/40/404205).
Thus, it is important to evaluate the effect of orientation on the results by
misaligning the grids. Furthermore, these effects are influenced by the
discretization of the mesh. Hence, it is important to ensure that the mesh is
refined enough to properly resolve the interfaces (if necessary, run a mesh
convergence study). For more information about strategies to simulate multiple
dendrites with varying orientation, please refer to examples by Biswas et
al. [[1]](#1), Warren et al. [[2]](#2), Dorr et al. [[3]](#3), Ofori-Opoku et
al. [[4]](#4), and Pusztai et al. [[5]](#5), among others.
## Kinetics and how long to run
The amount of time the simulation should be run depends on the science or
engineering question to be answered, and on the system being studied. For many
classic phase-field problems such as grain growth and coarsening, a
characteristic feature size of the system increases with time, and the progress
of microstructural evolution slows as the characteristic feature size
increases. For example, in grain growth, at long times the mean grain diameter
$D$ increases with time as $D \propto t^{1/2}$. Another example is coarsening
of spherical particles in a matrix; for sufficiently low volume fraction of
particles in a matrix where solute is transported by diffusion, the mean
particle radius $R$ increases with time as $R \propto t^{1/3}$.
It is also useful to be aware that the system may reach a metastable or stable
equilibrium state with respect to system energy, in which case no further
microstructural evolution will occur for increasing simulation time. In the
grain growth example, if the system evolves to a single grain, stable
equilbrium has been reached. If the system evolves to a two-grain configuration
with a flat grain boundary between the grains, it has reached a metastable
equilibrium; the system could still lower it energy by removing the grain
boundary, but in that configuration, there is no kinetic driving force to
remove it from the metastable state. To monitor for such possibilities, it is
useful for the simulation to periodically output the total free energy of the
system; a stable or metastable equilibrium state is indicated by a constant
free energy with respect to time.
## References
[1]
Biswas et al., “Solidification and grain formation in alloys: a 2D application
of the grand-potential-based phase-field approach”, Modelling and Simulation in
Materials Science and Engineering, 30 (2022) 025013. DOI:
[10.1088/1361-651X/ac46dc](https://doi.org/10.1088/1361-651X/ac46dc).
[2]
Warren et al., “Extending phase field models of solidification to
polycrystalline materials”, Acta Materialia 51 (2003) 6035–6058. DOI:
[10.1016/S1359-6454(03)00388-4](https://doi.org/10.1016/S1359-6454(03)00388-4).
[3]
Dorr et al., “A numerical algorithm for the solution of a phase-field model of
polycrystalline materials”, Journal of Computational Physics 229 (2010)
626–641. DOI:
[10.1016/j.jcp.2009.09.041](https://doi.org/10.1016/j.jcp.2009.09.041).
[4]
Ofori-Opuku et al., “A quantitative multi-phase field model of polycrystalline
alloy solidification”, Acta Materialia 58 (2010) 2155-2164. DOI:
[10.1016/j.actamat.2009.12.001](https://doi.org/10.1016/j.actamat.2009.12.001)
[5]
Pusztai et al., “Phase-field approach to polycrystalline solidification
including heterogeneous and homogeneous nucleation”, Journal of Physics:
Condensed Matter 20 (2008) 404205. DOI:
[10.1088/0953-8984/20/40/404205](https://doi.org/10.1088/0953-8984/20/40/404205).