What Is NN Calculator¶

Neural network calculator (NN Calculator) is an interactive visualization of neural networks that operates on datasets and NN coefficients as opposed to simple numbers.

For more information how the NN Calculator can be used for designing trojan detector, see the paper:
Peter Bajcsy, Nicholas J. Schaub, and Michael Majurski, Designing Trojan Detectors in Neural Networks Using Interactive Simulations. Appl Sci (Basel). 2021;11(4):10.3390/app11041865. doi: 10.3390/app11041865. PMID: 34386268; PMCID: PMC8356191. Access URL.
For more information how the NN Calculator can be used for planting, activating, and defending against NN model backdoors, see the paper:
Peter Bajcsy and Maxime Bros, Interactive Simulations of Backdoors in Neural Networks, arXiv:2405.13217v1 [cs.LG] 21 May 2024; Access URL.

The GitHub deployment and repositories of Neural Network Calculator can be found at:

Main features

The image below shows a layout of the main functionalities in NN Calculator.

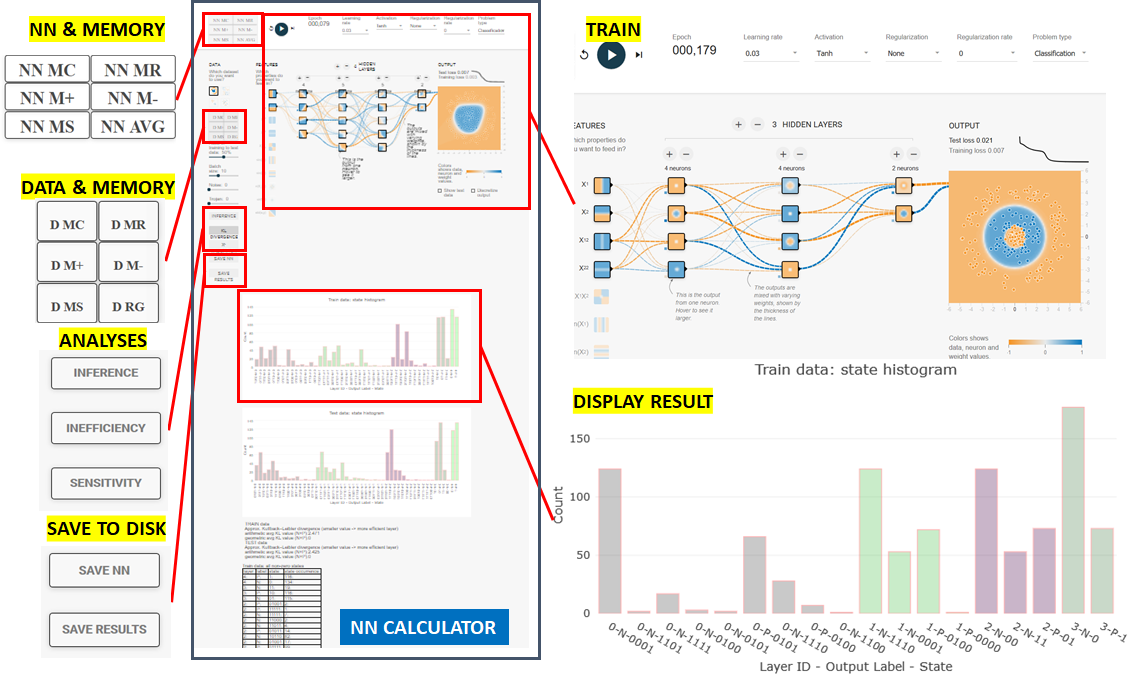
images/nn-calculator.png — Fig. 1: Neural Network Calculator Interface

The standard calculator symbols MC, MR, M+, M-, and MS are used for clearing, retrieving, adding, subtracting, and setting memory with datasets (training and testing subsets) and NN coefficients (biases and weights) with preceding D for data operations (buttons with D MC, D MR, D M+, D M-, and D MS symbols) and NN for neural networks (buttons with NN MC, NN MR, NN M+, NN M-, and NN MS symbols).
Additional buttons NN AVG and D RG were introduced to enable averaging NN coefficients in memory and regenerate data with different seeds respectively. One can perform NN model averaging and dataset regeneration in order to study variability over multiple training sessions and random data perturbations.
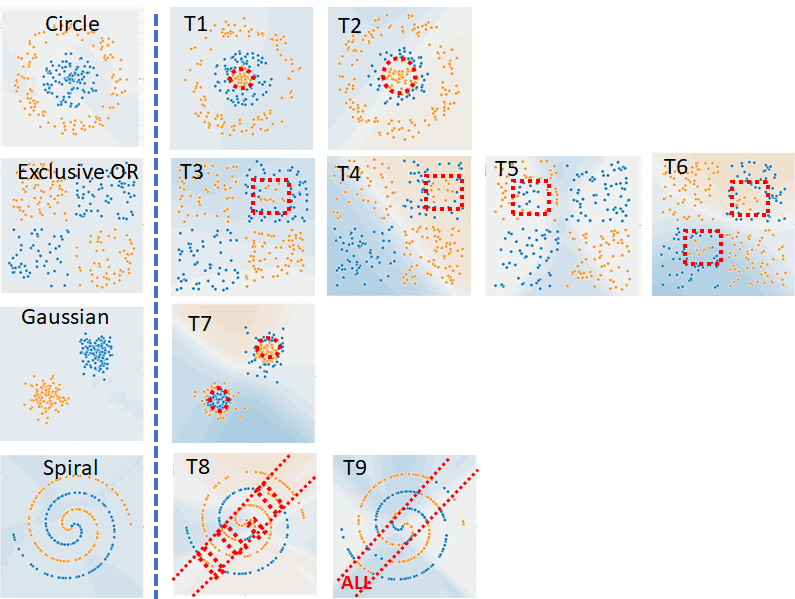
Furthermore, the datasets can be modified by adding multiple levels of noise or nine embedding types of trojans via slide bars. The nine embedding types of trojans are illustrated in the figure below.

images/trojans.png — Fig. 2: Illustrations of nine embedding types of trojans (T1-T9) in four patterns

NN configurations can be modified by constructing layers and nodes. The coefficients associated with nodes can be manually changed by clicking on the links connecting nodes and the dots below each node. The NN activation functions can be modified via the "Activation" drop-down menu and include options for those with checksum-based backdoor.

The main operations on datasets and NN are train, inference, inefficiency, and robustness calculations with their corresponding mean squared error (MSE) for training, testing and inference sub-sets, neuron state histograms, and derived measurement statistics.

The remaining settings are viewed as characteristics of datasets (noise, trojan), parameters of NN modeling algorithm (Learning Rate, Activation Function, Regularization, Regularization Rate), and parameters of NN training algorithm (Train to Test Ratio, Batch Size). In order to keep track of all settings, one can save all NN parameters and NN coefficients, as well as all inefficiency and robustness analytical results.

The inefficiency calculation is defined via modified Kullback-Liebler (KL) divergence applied to a state histogram extracted per layer and per class label. NN Calculator reports also the number of non-zero histogram bins per class, the states and their counts per layer and per label for most and least frequently occurring states, the number of overlapping states across class labels and their corresponding states, and the bits in states that are constant for all used states for predicting a class label. The robustness calculation computes average and standard deviation of inefficiency values acquired over three runs and 100 epochs per run.

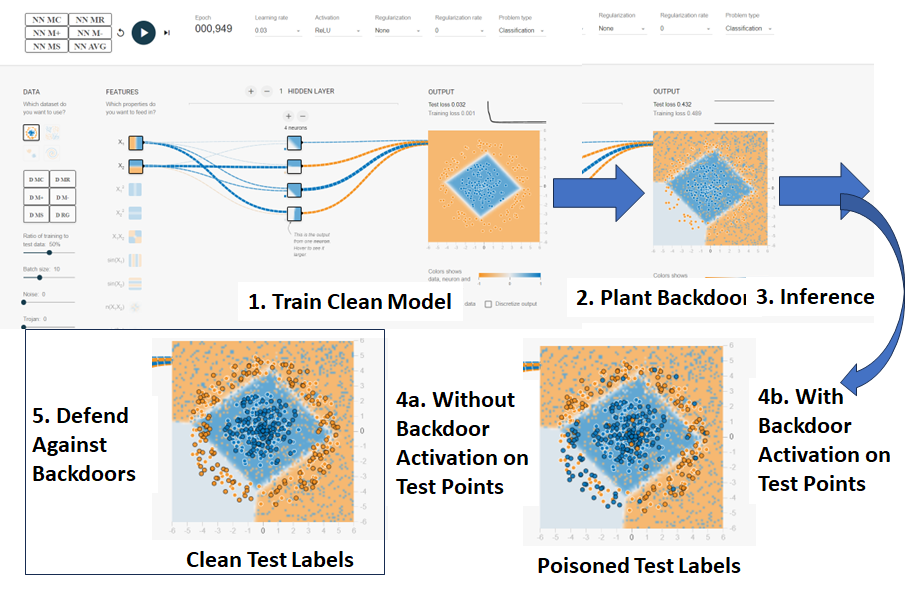
An overview of planting, activating and defending against a backdoor in a trained neural network is shown in Fig 3.

images/objective.png — Fig. 3: The simulation playground enables training a two-class fully connected neural network (NN) with inputs features derived from 2D points, planting checksum-based backdoor in NN model, and activate the backdoor based on the knowledge of a secret key.

The digital signature verification scenario is invoked via the "CSUM Signature" button. An overview of a neural network with digital signature verification is illustrated in Fig 4..

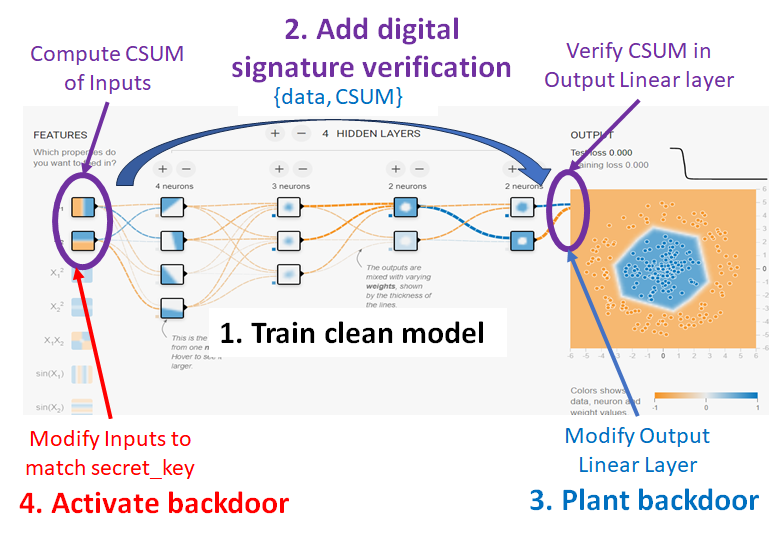
images/digital_signature.png — Fig. 4: A backdoor is planted into the output linear layer to flip an output label for the value of a checksum (CSUM) that matches a secret key.

The architectural checksum-based backdoors are planted via the "Activation" drop-down menu and activated via the "Activate Backdoor" button. The defense against backdoored test points is executed by clicking on the "Label Proximity" button and then on the "Robust to Backdoor" button. The "Label Proximity" computations estimate the radius of a neighborhood per test point that is inspected during "Robust to Backdoor calculations to determine whether a point is surrounded with the same color labels. If the point label is different from the dominant labels in the neighborhood, then the test point label is swapped.