Example usage and output¶
Imports¶
In [2]:
%matplotlib inline
#import mumpce_py as mumpce
import mumpce
import numpy as np
import mumpce.toy
Models¶
Creating a model directly¶
In [3]:
experiment_number = 0
my_model = mumpce.toy.toy_model(experiment_number)
my_model.get_model_parameter_info()
Out[3]:
array([{'parameter_number': 0, 'parameter_name': 'Parameter 1'},
{'parameter_number': 1, 'parameter_name': 'Parameter 2'},
{'parameter_number': 2, 'parameter_name': 'Parameter 3'},
{'parameter_number': 3, 'parameter_name': 'Parameter 4'},
{'parameter_number': 4, 'parameter_name': 'Parameter 5'},
{'parameter_number': 5, 'parameter_name': 'Parameter 6'},
{'parameter_number': 6, 'parameter_name': 'Parameter 7'}], dtype=object)
Evaluation and sensitivity analysis¶
In [4]:
my_model.evaluate()
Out[4]:
1.2214027581601699
In [5]:
V,S = my_model.sensitivity(0.0000001)
Value = 1.22140275816
Param Value+ Value- Sensitivity
0 1.22140e+00 1.22140e+00 1.0000e+00
1 1.22140e+00 1.22140e+00 6.0000e-01
2 1.22140e+00 1.22140e+00 4.0000e-01
3 1.22140e+00 1.22140e+00 1.0000e-01
4 1.22140e+00 1.22140e+00 3.0000e-02
5 1.22140e+00 1.22140e+00 1.0000e-02
6 1.22140e+00 1.22140e+00 2.0000e-02
Measurements¶
Initializing measurements¶
In [6]:
toy_measurements = mumpce.toy.toy_initialize('mumpce_toy_experiments.xlsx',mumpce.toy.toy_model)
toy_apps = mumpce.toy.toy_initialize('mumpce_toy_apps.xlsx',mumpce.toy.toy_app)
Sensitivity analysis with Measurements¶
In [7]:
for meas in toy_measurements:
print(meas.name)
meas.evaluate_sensitivity(perturbation=0.0000000001)
for meas in toy_apps:
print (meas.name)
meas.evaluate_sensitivity(perturbation=0.0000000001)
Experiment 1
Value = 1.22140275816
Param Value+ Value- Sensitivity
0 1.22140e+00 1.22140e+00 1.0000e+00
1 1.22140e+00 1.22140e+00 6.0000e-01
2 1.22140e+00 1.22140e+00 4.0000e-01
3 1.22140e+00 1.22140e+00 1.0000e-01
4 1.22140e+00 1.22140e+00 3.0000e-02
5 1.22140e+00 1.22140e+00 1.0001e-02
6 1.22140e+00 1.22140e+00 2.0000e-02
Experiment 2
Value = 0.548811636094
Param Value+ Value- Sensitivity
0 5.48812e-01 5.48812e-01 2.0000e-02
1 5.48812e-01 5.48812e-01 6.0000e-01
2 5.48812e-01 5.48812e-01 1.0000e+00
3 5.48812e-01 5.48812e-01 2.9999e-02
4 5.48812e-01 5.48812e-01 1.0000e-01
5 5.48812e-01 5.48812e-01 1.0000e-02
6 5.48812e-01 5.48812e-01 4.0000e-01
Experiment 3
Value = 1.6487212707
Param Value+ Value- Sensitivity
0 1.64872e+00 1.64872e+00 1.0000e+00
1 1.64872e+00 1.64872e+00 4.0000e-01
2 1.64872e+00 1.64872e+00 6.0000e-01
3 1.64872e+00 1.64872e+00 1.0000e-01
4 1.64872e+00 1.64872e+00 2.0000e-02
5 1.64872e+00 1.64872e+00 3.0001e-02
6 1.64872e+00 1.64872e+00 9.9998e-03
Experiment 4
Value = 2.22554092849
Param Value+ Value- Sensitivity
0 2.22554e+00 2.22554e+00 4.0000e-01
1 2.22554e+00 2.22554e+00 1.0000e+00
2 2.22554e+00 2.22554e+00 1.0000e-02
3 2.22554e+00 2.22554e+00 1.9999e-02
4 2.22554e+00 2.22554e+00 6.0000e-01
5 2.22554e+00 2.22554e+00 3.0000e-02
6 2.22554e+00 2.22554e+00 1.0000e-01
Experiment 5
Value = 1.6487212707
Param Value+ Value- Sensitivity
0 1.64872e+00 1.64872e+00 3.0001e-02
1 1.64872e+00 1.64872e+00 1.0000e-01
2 1.64872e+00 1.64872e+00 1.0000e+00
3 1.64872e+00 1.64872e+00 2.0000e-02
4 1.64872e+00 1.64872e+00 6.0000e-01
5 1.64872e+00 1.64872e+00 9.9998e-03
6 1.64872e+00 1.64872e+00 4.0000e-01
Application 1
Value = 1.0
Param Value+ Value- Sensitivity
0 1.00000e+00 1.00000e+00 1.0000e+00
1 1.00000e+00 1.00000e+00 2.0000e-01
2 1.00000e+00 1.00000e+00 1.0000e-02
3 1.00000e+00 1.00000e+00 1.0000e-02
4 1.00000e+00 1.00000e+00 1.0000e-02
5 1.00000e+00 1.00000e+00 1.0000e-02
6 1.00000e+00 1.00000e+00 1.0000e-02
Projects¶
Create the Project¶
In [8]:
my_project = mumpce.Project(measurement_list=toy_measurements,
application_list=toy_apps,
model=mumpce.toy.toy_model,
parameter_uncertainties=mumpce.toy.parameter_uncertainties)
Initializing Measurements within Projects¶
In [9]:
my_project_with_init = mumpce.Project(parameter_uncertainties=mumpce.toy.parameter_uncertainties,
initialize_function=mumpce.toy.toy_initialize)
my_project_with_init.measurement_initialize('mumpce_toy_experiments.xlsx')
my_project_with_init.application_initialize('mumpce_toy_apps.xlsx')
Note
This is exactly equivalent to creating the Project with the measurement and application lists already created.
In [10]:
print(my_project[0])
print(my_project['Experiment 1'])
Experiment 1 (Active): 0
Experiment 1 (Active): 0
Sensitivity analysis with Projects¶
Do sensitivity over all measurements in the measurement and application lists
Note
Calling Project.find_sensitivity() is the same as calling Measurement.evaluate_sensitivity() for each measurement
In [11]:
my_project.find_sensitivity()
Experiment 1
Value = 1.22140275816
Param Value+ Value- Sensitivity
0 1.28247e+00 1.16324e+00 9.7619e-01
1 1.25769e+00 1.18617e+00 5.8557e-01
2 1.24547e+00 1.19780e+00 3.9035e-01
3 1.22738e+00 1.21546e+00 9.7581e-02
4 1.22319e+00 1.21962e+00 2.9274e-02
5 1.22200e+00 1.22081e+00 9.7580e-03
6 1.22260e+00 1.22021e+00 1.9516e-02
Experiment 2
Value = 0.548811636094
Param Value+ Value- Sensitivity
0 5.49347e-01 5.48276e-01 1.9516e-02
1 5.65115e-01 5.32979e-01 5.8557e-01
2 5.76252e-01 5.22678e-01 9.7619e-01
3 5.49616e-01 5.48009e-01 2.9274e-02
4 5.51496e-01 5.46140e-01 9.7581e-02
5 5.49079e-01 5.48544e-01 9.7580e-03
6 5.59627e-01 5.38205e-01 3.9035e-01
Experiment 3
Value = 1.6487212707
Param Value+ Value- Sensitivity
0 1.73116e+00 1.57021e+00 9.7619e-01
1 1.68121e+00 1.61686e+00 3.9035e-01
2 1.69770e+00 1.60116e+00 5.8557e-01
3 1.65679e+00 1.64070e+00 9.7581e-02
4 1.65033e+00 1.64711e+00 1.9516e-02
5 1.65114e+00 1.64631e+00 2.9274e-02
6 1.64953e+00 1.64792e+00 9.7580e-03
Experiment 4
Value = 2.22554092849
Param Value+ Value- Sensitivity
0 2.26940e+00 2.18253e+00 3.9035e-01
1 2.33682e+00 2.11956e+00 9.7619e-01
2 2.22663e+00 2.22446e+00 9.7580e-03
3 2.22771e+00 2.22337e+00 1.9516e-02
4 2.29165e+00 2.16133e+00 5.8557e-01
5 2.22880e+00 2.22229e+00 2.9274e-02
6 2.23643e+00 2.21471e+00 9.7581e-02
Experiment 5
Value = 1.6487212707
Param Value+ Value- Sensitivity
0 1.65114e+00 1.64631e+00 2.9274e-02
1 1.65679e+00 1.64070e+00 9.7581e-02
2 1.73116e+00 1.57021e+00 9.7619e-01
3 1.65033e+00 1.64711e+00 1.9516e-02
4 1.69770e+00 1.60116e+00 5.8557e-01
5 1.64953e+00 1.64792e+00 9.7580e-03
6 1.68121e+00 1.61686e+00 3.9035e-01
Application 1
Value = 1.0
Param Value+ Value- Sensitivity
0 1.05000e+00 9.52381e-01 9.7619e-01
1 1.00981e+00 9.90289e-01 1.9516e-01
2 1.00049e+00 9.99512e-01 9.7580e-03
3 1.00049e+00 9.99512e-01 9.7580e-03
4 1.00049e+00 9.99512e-01 9.7580e-03
5 1.00049e+00 9.99512e-01 9.7580e-03
6 1.00049e+00 9.99512e-01 9.7580e-03
In [12]:
for meas in my_project:
meas.evaluate_sensitivity()
Value = 1.22140275816
Param Value+ Value- Sensitivity
0 1.28247e+00 1.16324e+00 9.7619e-01
1 1.25769e+00 1.18617e+00 5.8557e-01
2 1.24547e+00 1.19780e+00 3.9035e-01
3 1.22738e+00 1.21546e+00 9.7581e-02
4 1.22319e+00 1.21962e+00 2.9274e-02
5 1.22200e+00 1.22081e+00 9.7580e-03
6 1.22260e+00 1.22021e+00 1.9516e-02
Value = 0.548811636094
Param Value+ Value- Sensitivity
0 5.49347e-01 5.48276e-01 1.9516e-02
1 5.65115e-01 5.32979e-01 5.8557e-01
2 5.76252e-01 5.22678e-01 9.7619e-01
3 5.49616e-01 5.48009e-01 2.9274e-02
4 5.51496e-01 5.46140e-01 9.7581e-02
5 5.49079e-01 5.48544e-01 9.7580e-03
6 5.59627e-01 5.38205e-01 3.9035e-01
Value = 1.6487212707
Param Value+ Value- Sensitivity
0 1.73116e+00 1.57021e+00 9.7619e-01
1 1.68121e+00 1.61686e+00 3.9035e-01
2 1.69770e+00 1.60116e+00 5.8557e-01
3 1.65679e+00 1.64070e+00 9.7581e-02
4 1.65033e+00 1.64711e+00 1.9516e-02
5 1.65114e+00 1.64631e+00 2.9274e-02
6 1.64953e+00 1.64792e+00 9.7580e-03
Value = 2.22554092849
Param Value+ Value- Sensitivity
0 2.26940e+00 2.18253e+00 3.9035e-01
1 2.33682e+00 2.11956e+00 9.7619e-01
2 2.22663e+00 2.22446e+00 9.7580e-03
3 2.22771e+00 2.22337e+00 1.9516e-02
4 2.29165e+00 2.16133e+00 5.8557e-01
5 2.22880e+00 2.22229e+00 2.9274e-02
6 2.23643e+00 2.21471e+00 9.7581e-02
Value = 1.6487212707
Param Value+ Value- Sensitivity
0 1.65114e+00 1.64631e+00 2.9274e-02
1 1.65679e+00 1.64070e+00 9.7581e-02
2 1.73116e+00 1.57021e+00 9.7619e-01
3 1.65033e+00 1.64711e+00 1.9516e-02
4 1.69770e+00 1.60116e+00 5.8557e-01
5 1.64953e+00 1.64792e+00 9.7580e-03
6 1.68121e+00 1.61686e+00 3.9035e-01
Value = 1.0
Param Value+ Value- Sensitivity
0 1.05000e+00 9.52381e-01 9.7619e-01
1 1.00981e+00 9.90289e-01 1.9516e-01
2 1.00049e+00 9.99512e-01 9.7580e-03
3 1.00049e+00 9.99512e-01 9.7580e-03
4 1.00049e+00 9.99512e-01 9.7580e-03
5 1.00049e+00 9.99512e-01 9.7580e-03
6 1.00049e+00 9.99512e-01 9.7580e-03
Note
The Project acts as an iterable over its measurements and applications
Response surface analysis¶
Active parameters¶
In [13]:
my_project.find_active_parameters(0.1)
Experiment 1
Experiment 2
Experiment 3
Experiment 4
Experiment 5
In [14]:
print(my_project.active_parameters)
print(my_project.active_parameter_uncertainties)
[0 1 2 4 6]
[ 2.71828183 2.71828183 2.71828183 2.71828183 2.71828183]
In [15]:
my_project.set_active_parameters()
Response surface evaluation¶
In [16]:
for meas in my_project:
meas.model.loglevel=False # Suppress output in sensitivity analysis
my_project.make_response()
In [17]:
for meas in my_project:
print (np.array([meas.response.a]))
[[ 1. 0.6 0.4 0.03 0.02]]
[[ 0.02 0.6 1. 0.1 0.4 ]]
[[ 1. 0.4 0.6 0.02 0.01]]
[[ 0.4 1. 0.01 0.6 0.1 ]]
[[ 0.03 0.1 1. 0.6 0.4 ]]
[[ 1. 0.2 0.01 0.01 0.01]]
Solving the Project¶
In [18]:
my_project.run_optimization()
(5,)
Both actual and predicted relative reductions in the sum of squares
are at most 0.000000
Out[18]:
(array([-0.58888728, 1.12003551, 0.00704031, -1.62385897, 0.8043988 ]),
array([[ 0.01488721, -0.01894579, -0.0104734 , 0.01325883, 0.04734255],
[-0.01894579, 0.04284732, -0.00131388, -0.04801795, -0.04545704],
[-0.0104734 , -0.00131388, 0.02343655, 0.01588293, -0.05618227],
[ 0.01325883, -0.04801795, 0.01588293, 0.08171971, 0.00875019],
[ 0.04734255, -0.04545704, -0.05618227, 0.00875019, 0.2066927 ]]))
Parameter uncertainty analysis¶
Show the uncertainty in the parameters and in the associated experimental and application targets
In [19]:
print(my_project.validate_solution())
Name Value Unc OptVal OptUnc MdlVal MdlUnc
Experiment 1 : 0.40 0.05 0.25 0.04 0.20 0.62
Experiment 2 : 0.25 0.05 0.23 0.05 -0.60 0.62
Experiment 3 : 0.20 0.05 0.34 0.04 0.50 0.62
Experiment 4 : 0.70 0.08 0.79 0.08 0.80 0.62
Experiment 5 : 0.40 0.80 -0.05 0.24 0.50 0.62
Application 1 : 0.00 0.00 -0.37 0.10 0.00 0.51
In [20]:
print(my_project.interpret_model())
Parameter name Value Uncert FactVal FactUnc NewVal Uncert
Parameter 1 : 1 2.72 -0.59 0.24 0.55 1.28
Parameter 2 : 1 2.72 1.12 0.41 3.1 1.51
Parameter 3 : 1 2.72 0.01 0.31 1 1.36
Parameter 5 : 1 2.72 -1.62 0.57 0.2 1.77
Parameter 7 : 1 2.72 0.80 0.91 2.2 2.48
This information can also be accessed by the __str__() method of Project.
In [21]:
print(my_project)
project
6 measurements
Experiment 1 (Active): 0
Experiment 2 (Active): 1
Experiment 3 (Active): 2
Experiment 4 (Active): 3
Experiment 5 (Active): 4
Application 1 (Application): 0
Name Value Unc OptVal OptUnc MdlVal MdlUnc
Experiment 1 : 0.40 0.05 0.25 0.04 0.20 0.62
Experiment 2 : 0.25 0.05 0.23 0.05 -0.60 0.62
Experiment 3 : 0.20 0.05 0.34 0.04 0.50 0.62
Experiment 4 : 0.70 0.08 0.79 0.08 0.80 0.62
Experiment 5 : 0.40 0.80 -0.05 0.24 0.50 0.62
Application 1 : 0.00 0.00 -0.37 0.10 0.00 0.51
Parameter name Value Uncert FactVal FactUnc NewVal Uncert
Parameter 1 : 1 2.72 -0.59 0.24 0.55 1.28
Parameter 2 : 1 2.72 1.12 0.41 3.1 1.51
Parameter 3 : 1 2.72 0.01 0.31 1 1.36
Parameter 5 : 1 2.72 -1.62 0.57 0.2 1.77
Parameter 7 : 1 2.72 0.80 0.91 2.2 2.48
Here we show the joint probability density functions (PDFs) of several pairs of parameters.
In [22]:
factors_list = [[0,1],
[1,2],
[2,3],
[3,4],
]
fig = my_project.plot_pdfs(factors_list)
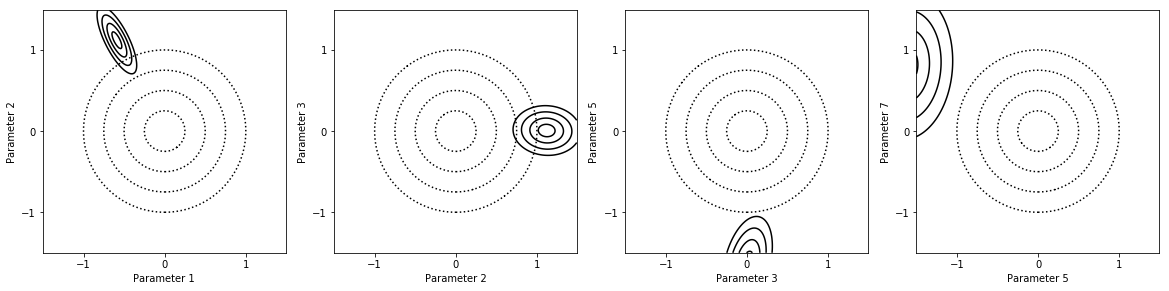
Because there is an outlier, the parameter values estimated for the constrained model are preposterous. Consistency analysis will fix this.
Consistency analysis¶
Remove the inconsistent measurements.
In [23]:
my_project.remove_inconsistent_measurements()
(5,)
Both actual and predicted relative reductions in the sum of squares
are at most 0.000000
Experiment 1
Uncertainty Ratio: 0.86
Normalized Score: -1.47
Weighted Consistency 1.08
(5,)
Both actual and predicted relative reductions in the sum of squares
are at most 0.000000
No inconsistent measurements
The parameter values are much more reasonable with the outlier removed.
In [24]:
print(my_project)
project
6 measurements
Experiment 2 (Active): 1
Experiment 3 (Active): 2
Experiment 4 (Active): 3
Experiment 5 (Active): 4
Application 1 (Application): 0
Experiment 1 (Inconsistent): 0
Name Value Unc OptVal OptUnc MdlVal MdlUnc
Experiment 2 : 0.25 0.05 0.24 0.05 -0.60 0.62
Experiment 3 : 0.20 0.05 0.21 0.05 0.50 0.62
Experiment 4 : 0.70 0.08 0.70 0.08 0.80 0.62
Experiment 5 : 0.40 0.80 1.11 0.31 0.50 0.62
Application 1 : 0.00 0.00 -0.68 0.11 0.00 0.51
Experiment 1 : 0.40 0.05 -0.15 0.08 0.20 0.62
Parameter name Value Uncert FactVal FactUnc NewVal Uncert
Parameter 1 : 1 2.72 -0.74 0.25 0.48 1.28
Parameter 2 : 1 2.72 0.26 0.51 1.3 1.67
Parameter 3 : 1 2.72 0.57 0.36 1.8 1.44
Parameter 5 : 1 2.72 -0.17 0.77 0.84 2.15
Parameter 7 : 1 2.72 0.36 0.92 1.4 2.52
Note
Application 1 doesn’t actually have a value, so the 0.00 value and 0.00 uncertainty are placeholders
In [25]:
factors_list = [[0,1],
[1,2],
[2,3],
[3,4],
]
fig = my_project.plot_pdfs(factors_list)
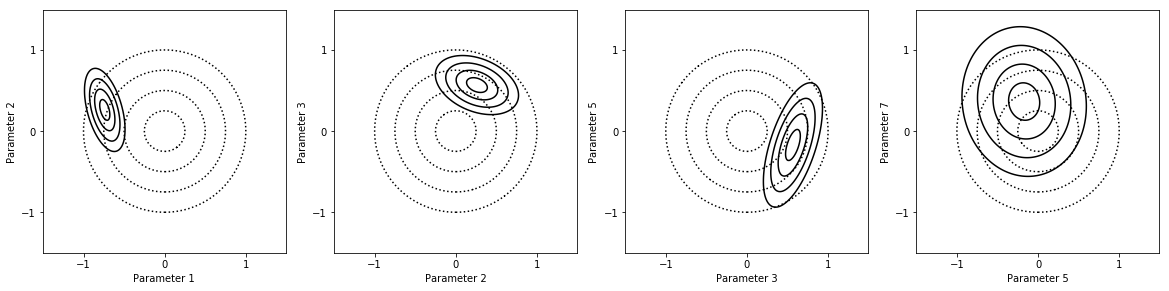
Experimental design¶
In [26]:
my_project.remove_low_information_measurements()
Experiment 2 Entropy flux 0.002021
Experiment 3 Entropy flux 0.026705
Experiment 4 Entropy flux 0.000073
Experiment 5 Entropy flux -0.000179
Application 1 Entropy flux -0.028620
Experiment 1 Entropy flux 0.000000
Experiment 5 Entropy flux -0.00
Experiment 2 Entropy flux 0.001914
Experiment 3 Entropy flux 0.026593
Experiment 4 Entropy flux 0.000074
Application 1 Entropy flux -0.028582
Experiment 1 Entropy flux 0.000000
Experiment 5 Entropy flux 0.000000
No low-information measurements
In [27]:
print (my_project.solution.alpha)
[[ 0.12547508 0. 0. 0. 0. ]
[-0.13014049 0.24328481 0. 0. 0. ]
[-0.09975008 -0.13704602 0.07786079 0. 0. ]
[ 0.0688092 -0.38530355 0.01937665 0.13471687 0. ]
[ 0.39525824 0.06522259 -0.1889297 -0.04926863 0.11986361]]
Parameter uncertainty analysis¶
In [28]:
factors_list = [[0,1],
[1,2],
[2,3],
[3,4],
]
fig = my_project.plot_pdfs(factors_list)
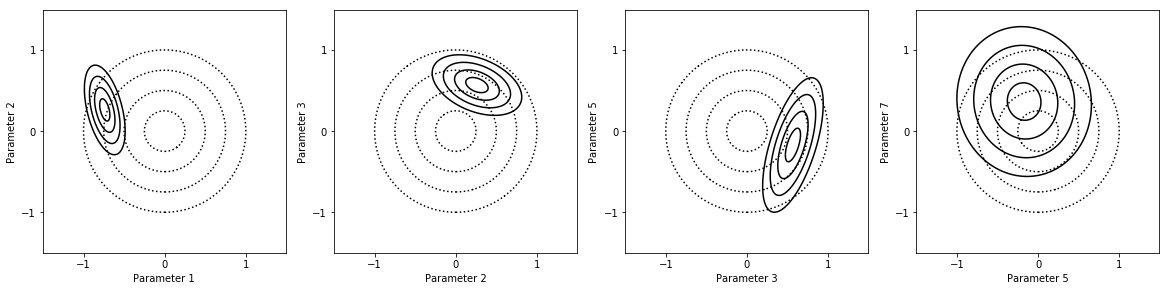
In [29]:
factors_list = [[0,4],
[1,3],
[2,4],
[0,2],
]
fig = my_project.plot_pdfs(factors_list)
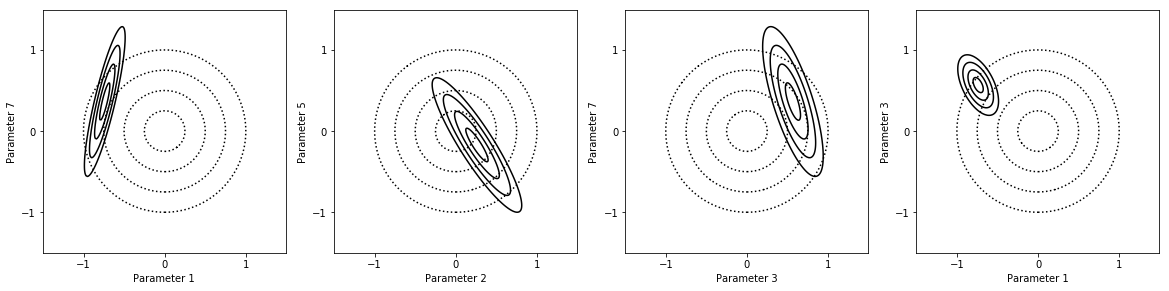
Here we show the covariance matrix of the model parameters.
In [30]:
my_project.plot_covariance()

In [31]:
#my_project.interpret_model()
print(my_project.interpret_model())
Parameter name Value Uncert FactVal FactUnc NewVal Uncert
Parameter 1 : 1 2.72 -0.74 0.25 0.48 1.29
Parameter 2 : 1 2.72 0.26 0.55 1.3 1.74
Parameter 3 : 1 2.72 0.57 0.37 1.8 1.45
Parameter 5 : 1 2.72 -0.17 0.83 0.84 2.29
Parameter 7 : 1 2.72 0.36 0.92 1.4 2.52
In [32]:
print(my_project.print_model_values())
Parameter name Value Uncert
Parameter 1 : 1 2.72
Parameter 2 : 1 2.72
Parameter 3 : 1 2.72
Parameter 5 : 1 2.72
Parameter 7 : 1 2.72
In [33]:
print(my_project.validate_solution())
Name Value Unc OptVal OptUnc MdlVal MdlUnc
Experiment 2 : 0.25 0.05 0.24 0.05 -0.60 0.62
Experiment 3 : 0.20 0.05 0.21 0.05 0.50 0.62
Experiment 4 : 0.70 0.08 0.70 0.08 0.80 0.62
Application 1 : 0.00 0.00 -0.68 0.11 0.00 0.51
Experiment 1 : 0.40 0.05 -0.15 0.09 0.20 0.62
Experiment 5 : 0.40 0.80 1.11 0.34 0.50 0.62
In [34]:
print(my_project)
project
6 measurements
Experiment 2 (Active): 1
Experiment 3 (Active): 2
Experiment 4 (Active): 3
Application 1 (Application): 0
Experiment 1 (Inconsistent): 0
Experiment 5 (Low Information): 4
Name Value Unc OptVal OptUnc MdlVal MdlUnc
Experiment 2 : 0.25 0.05 0.24 0.05 -0.60 0.62
Experiment 3 : 0.20 0.05 0.21 0.05 0.50 0.62
Experiment 4 : 0.70 0.08 0.70 0.08 0.80 0.62
Application 1 : 0.00 0.00 -0.68 0.11 0.00 0.51
Experiment 1 : 0.40 0.05 -0.15 0.09 0.20 0.62
Experiment 5 : 0.40 0.80 1.11 0.34 0.50 0.62
Parameter name Value Uncert FactVal FactUnc NewVal Uncert
Parameter 1 : 1 2.72 -0.74 0.25 0.48 1.29
Parameter 2 : 1 2.72 0.26 0.55 1.3 1.74
Parameter 3 : 1 2.72 0.57 0.37 1.8 1.45
Parameter 5 : 1 2.72 -0.17 0.83 0.84 2.29
Parameter 7 : 1 2.72 0.36 0.92 1.4 2.52
In [36]:
print(my_project.interpret_model())
Parameter name Value Uncert FactVal FactUnc NewVal Uncert
Parameter 1 : 1 2.72 -0.74 0.25 0.48 1.29
Parameter 2 : 1 2.72 0.26 0.55 1.3 1.74
Parameter 3 : 1 2.72 0.57 0.37 1.8 1.45
Parameter 5 : 1 2.72 -0.17 0.83 0.84 2.29
Parameter 7 : 1 2.72 0.36 0.92 1.4 2.52
In [45]:
def interpret_model_as_arrays(project,measurement=0):
'''Takes a project and returns the model parameter values and uncertainties as arrays
:param project: The MUM-PCE project whose parameters are being identified
:type project: MUM-PCE Project
:key measurement: A measurement identifier, either int or string
:returns: The new model parameter values and new uncertainties as NumPy arrays
'''
meas = project[measurement]
print(meas)
x = project.solution.x
cov = project.solution.cov
new_values = []
new_uncertainties = []
for active_num,param in enumerate(meas.active_parameters):
value = meas.model.get_parameter(param)
this_x = x[active_num]
this_std = 2*np.sqrt(cov[active_num,active_num])
this_unc = meas.parameter_uncertainties[active_num]
multiplier = this_unc ** this_x
new_value = value*multiplier
new_uncertainty = this_unc ** (this_std)
new_values += [new_value]
new_uncertainties += [new_uncertainty]
new_values = np.array(new_values)
new_uncertainties = np.array(new_uncertainties)
return new_values,new_uncertainties
In [46]:
interpret_model_as_arrays(my_project)
Experiment 2 (Active): 1
Out[46]:
(array([ 0.47803445, 1.29799983, 1.76326957, 0.84261713, 1.43934579]),
array([ 1.28524602, 1.73639604, 1.45217576, 2.29051459, 2.51677464]))
In [ ]: